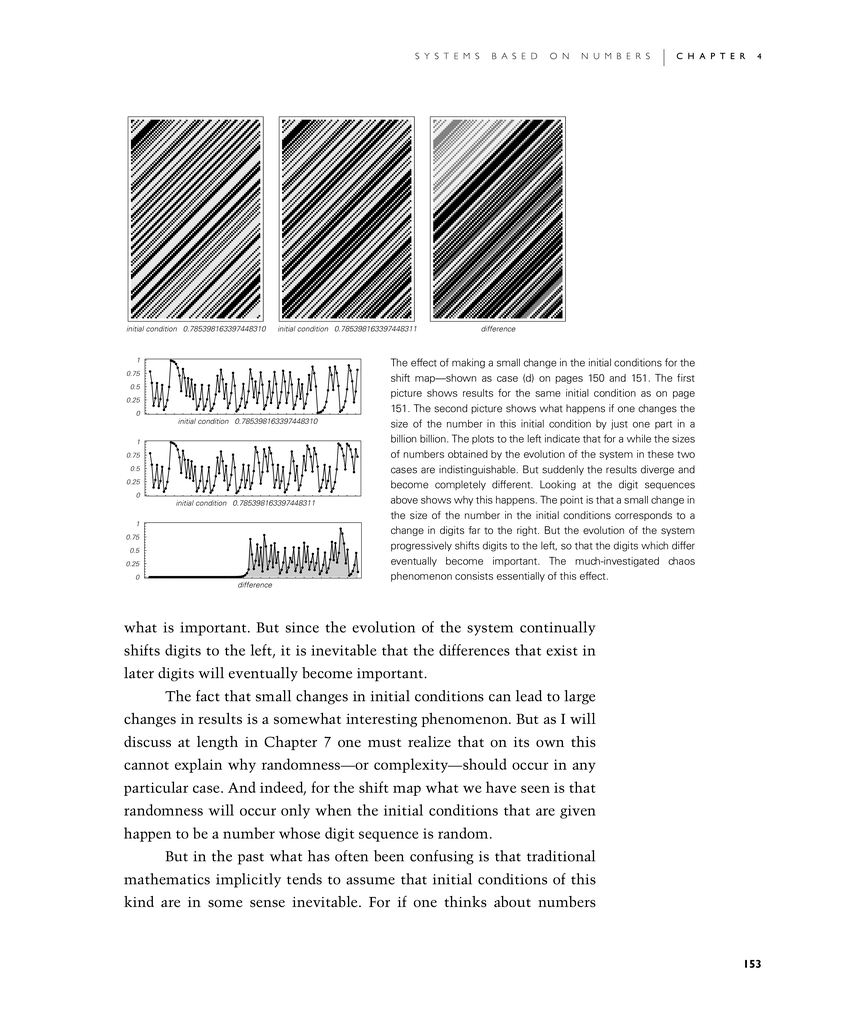
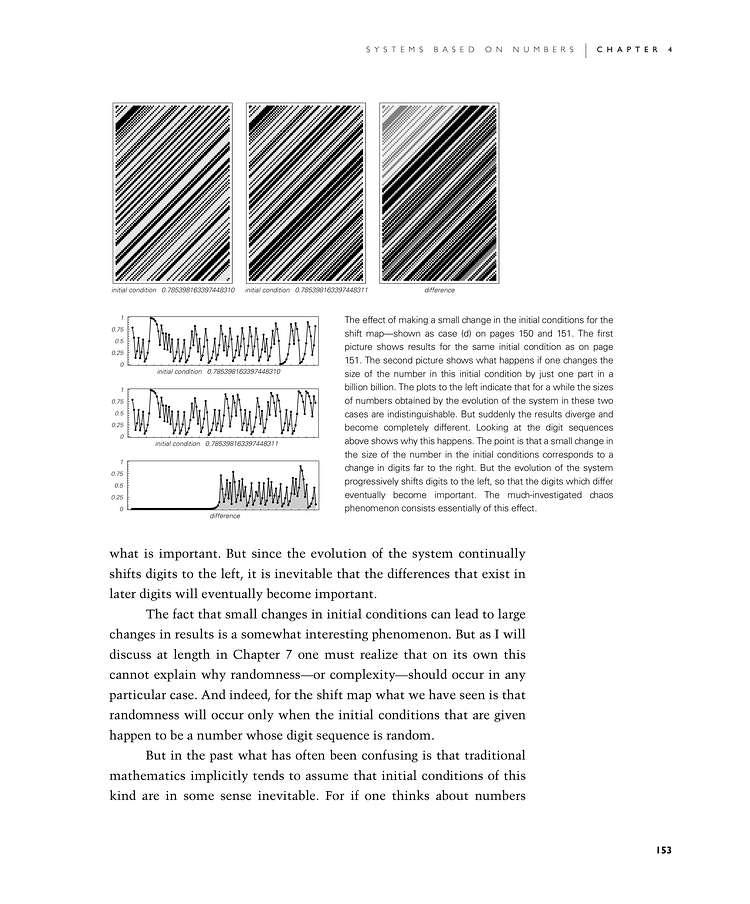
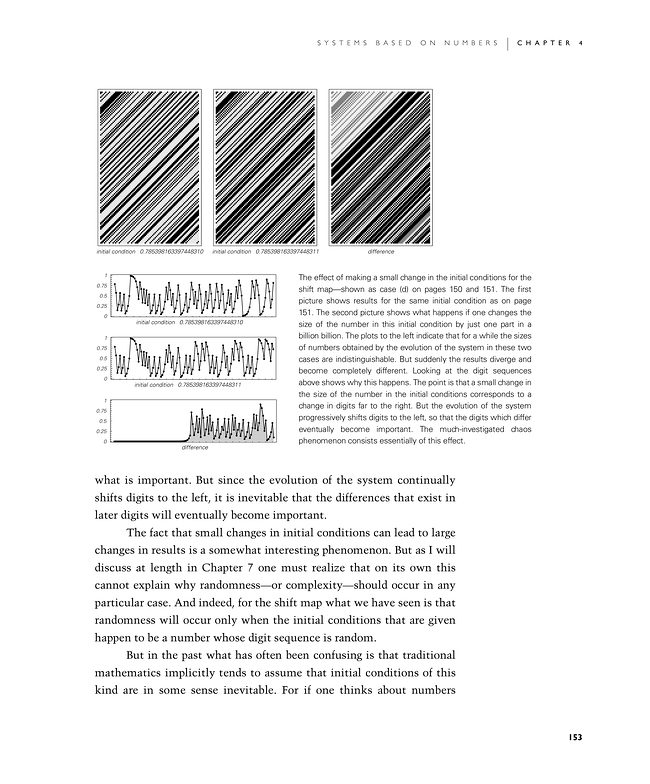
what is important. But since the evolution of the system continually shifts digits to the left, it is inevitable that the differences that exist in later digits will eventually become important.

The fact that small changes in initial conditions can lead to large changes in results is a somewhat interesting phenomenon. But as I will discuss at length in Chapter 7 one must realize that on its own this cannot explain why randomness—or complexity—should occur in any particular case. And indeed, for the shift map what we have seen is that randomness will occur only when the initial conditions that are given happen to be a number whose digit sequence is random.

But in the past what has often been confusing is that traditional mathematics implicitly tends to assume that initial conditions of this kind are in some sense inevitable. For if one thinks about numbers

The effect of making a small change in the initial conditions for the shift map—shown as case (d) on pages 150 and 151. The first picture shows results for the same initial condition as on page 151. The second picture shows what happens if one changes the size of the number in this initial condition by just one part in a billion billion. The plots in the second picture indicate that for a while the sizes of numbers obtained by the evolution of the system in these two cases are indistinguishable. But suddenly the results diverge and become completely different. Looking at the digit sequences in the first picture shows why this happens. The point is that a small change in the size of the number in the initial conditions corresponds to a change in digits far to the right. But the evolution of the system progressively shifts digits to the left, so that the digits which differ eventually become important. The much-investigated chaos phenomenon consists essentially of this effect.