SOME HISTORICAL NOTES From: Stephen Wolfram, A New Kind of Science Notes for Chapter 9: Fundamental Physics Section: The Phenomenon of Gravity Page 1054 Quantum gravity. That there should be quantum effects in gravity was already noted in the 1910s, and when quantum field theory began to develop in the 1930s, there were immediately attempts to apply it to gravity. The first idea was to represent gravity as a field that exists in flat spacetime, and by analogy with photons in quantum electrodynamics to introduce gravitons (at one point identified with neutrinos). By the mid-1950s a path integral (see page 1066) based on the Einstein-Hilbert action had been constructed, and by the early 1960s Feynman diagram rules had been derived, and it had been verified that tree diagrams involving gravitons gave results that agreed with general relativity for small gravitational fields. But as soon as loop diagrams were considered, infinities began to appear. And unlike for quantum electrodynamics there did not seem to be only a finite number of these - that could be removed by renormalization. And in fact by 1973 gravity coupled to matter had been shown for certain not to be renormalizable - and the same was finally shown for pure gravity in 1986. There was an attempt in the 1970s and early 1980s to look directly at the path integral - without doing an expansion in terms of Feynman diagrams. But despite the fact that at least in Euclidean spacetime a variety of seemingly relevant field configurations were identified, many mathematical difficulties were encountered. And in the late-1970s there began to be interest in the idea that supersymmetric field theories might make infinities associated with gravitons be cancelled by ones associated with other particles. But in the end this did not work out. And then in the mid-1980s one of the great attractions of string theory was that it seemed to support graviton excitations without the problem of infinities seen in point-particle field theories. But it had other problems, and to avoid these, supersymmetry had to be introduced, leading to the presence of many other particles that have so far not been observed. (See also page 1033.) Starting in the 1950s a rather different approach to quantum gravity involved trying to find a representation of the structure of spacetime in which a quantum analog of the Einstein equations could be obtained by the formal procedure of canonical quantization (see page 1062). Yet despite a few signs of progress in the 1960s there was great difficulty in finding appropriately independent variables to use. In the late 1980s, however, it was suggested that variables could be used corresponding roughly to gravitational fluxes through loops in space. And in terms of these loop variables it was at least formally possible to write down a version of quantum gravity. Yet while this was found in the 1990s to have a correspondence with spin networks (see below), it has remained impossible to see just how it might yield ordinary general relativity as a limit. Even if one assumes that spacetime is in a sense ultimately continuous one can imagine investigating quantum gravity by doing some kind of discrete approximation. And in 1961 Tullio Regge noted that for a simplicial complex (see page 1055) the Einstein-Hilbert action has a rather simple form in terms of angles between edges. Starting in the 1980s after the development of lattice gauge theories, simulations of random surfaces and higher-dimensional spaces set up in this way were done - often using so-called dynamic triangulation based on random sequences of generalized Alexander moves from page 1042. But there were difficulties with Lorentzian spaces, and when large-scale average behavior was studied, it seemed difficult to reproduce observed smooth spacetime. Analytical approaches (that happened to be like 0D string theory) were also found for 2D discrete space× (compare page 1043) - but they were not successfully extended to higher dimensions. Over the years, various attempts have been made to derive quantum gravity from fundamentally discrete models of spacetime (compare page 1031). In recent × the most widely discussed have been spin networks - which despite their name ultimately seem to have fairly little to do with the systems I consider. Spin networks were introduced in 1964 by Roger Penrose as a way to set up an intrinsically quantum mechanical model of spacetime. A simple analog involves a 2D surface made out of triangles whose edges have integer lengths ji. If one computes the product of Exp[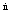 (j1+j2-j3)] for all triangles, then it turns out for example that this quantity is extremized exactly when the whole surface is flat. In 3D one imagines breaking space into tetrahedra whose edge lengths correspond to discrete quantum spin values. And in 1968 Tullio Regge and Giorgio Ponzano suggested - almost as an afterthought in technical work on 6j symbols - that the quantum probability amplitude for any form of space might perhaps be given by the product of 6j symbols for the spins on each tetrahedron. The SixJSymbol[{j1,j2,j3},{j4,j5,j6}] are slightly esoteric objects that correspond to recoupling coefficients for the 3D rotation group SO(3), and that arose in 1940s studies of combinations of three angular momenta in atomic physics - and were often represented graphically as networks. For large ji they are approximated by Cos[θ+π/4]/Sqrt[12 π v], where v is the volume of the tetrahedron and θ is a deficit angle. And from this it turns out that limits of products of 6j symbols correspond essentially to Exp[I s], where s is the discrete form of the Einstein-Hilbert action - extremized by flat 3D space. (The picture below shows for example Abs[SixJSymbol[{j,j,j},{j,j,j}]]. Note that for any j the 6j symbols can be given in terms of HypergeometricPFQ.) In the early 1990s there was again interest in spin networks when the Turaev-Viro invariant for 3D spaces was discovered from a topological field theory involving triangulations weighted with 6j symbols of the quantum group SU(2)q - and it was seen that invariance under Alexander moves on the triangulation corresponded to the Biedenharn-Elliott identity for 6j symbols. In the mid-1990s it was then found that states in 3D loop quantum gravity (see above) could be represented in terms of spin networks - leading for example to quantization of all areas and volumes. In attempting extensions to 4D, spin foams have been introduced - and variously interpreted in terms of simplified Feynman diagrams, constructs in multidimensional category theory, and possible evolutions of spin networks. In all cases, however, spin networks and spin foams seem to be viewed just as calculational constructs that must be evaluated and added together to get quantum amplitudes - quite different from my idea of associating an explicit evolution history for the universe with the evolution of a network. Stephen Wolfram, A New Kind of Science (Wolfram Media, 2002), page 1054. © 2002, Stephen Wolfram, LLC