SOME HISTORICAL NOTES

From: Stephen Wolfram, A New Kind of Science
Notes for Chapter 7: Mechanisms in Programs and Nature
Section: Chaos Theory and Randomness from Initial Conditions
Page 972

Three-body problem. The two-body problem was analyzed by Johannes Kepler in 1609 and solved by Isaac Newton in 1687. The three-body problem was a central topic in mathematical physics from the mid-1700s until the early 1900s. Various exact results were obtained - notably the existence of stable equilateral triangle configurations corresponding to so-called Lagrange points. Many approximate practical calculations, particularly on the Earth-Moon-Sun system, were done using series expansions involving thousands of algebraic terms. (It is now possible to get most results just by direct numerical computation using for example NDSolve.) From its basic setup the three-body system conserves standard mechanical quantities like energy and angular momentum. But it was thought it might also conserve other quantities (or so-called integrals of the motion). In 1887, however, Heinrich Bruns showed that there could be no such quantities expressible as algebraic functions of the positions and velocities of the bodies (in standard Cartesian coordinates). In the mid-1890s Henri Poincaré then showed that there could also be no such quantities analytic in positions, velocities and mass ratios. And from these results the conclusion was drawn that the three-body problem could not be solved in terms of algebraic formulas and integrals. In 1912 Karl Sundman did however find an infinite series that could in principle be summed to give the solution - but which converges exceptionally slowly. And even now it remains conceivable that the three-body problem could be solved in terms of more sophisticated standard mathematical functions. But I strongly suspect that in fact nothing like this will ever be possible and that instead the three-body problem will turn out to show the phenomenon of computational irreducibility discussed in Chapter 12 (and that for example three-body systems are universal and in effect able to perform any computation). (See also page 1138.)

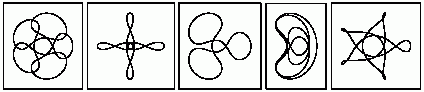
In Henri Poincaré’s study of the collection of possible trajectories for three-body systems he identified sensitive dependence on initial conditions (see above), noted the general complexity of what could happen (particularly in connection with so-called homoclinic tangles), and developed topology to provide a simpler overall description. With appropriate initial conditions one can get various forms of simple behavior. The pictures below show some of the possible repetitive orbits of an idealized planet moving in the plane of a pair of stars that are in a perfect elliptical orbit.

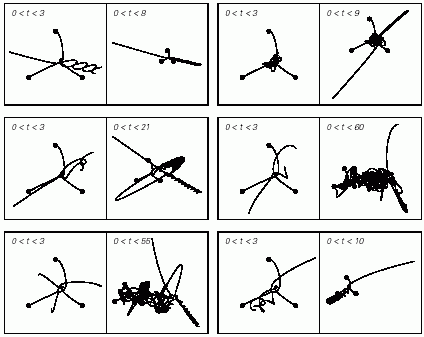
The pictures below show results for a fairly typical sequence of initial conditions where all three bodies interact. (The two bodies at the bottom are initially at rest; the body at the top is given progressively larger rightward velocities.) What generically happens is that one of the bodies escapes from the other two (like t or some× t^(2/3)). Often this happens quickly, but some× all three bodies show complex and apparently random behavior for quite a while. (The delay before escaping is reminiscent of resonant scattering.