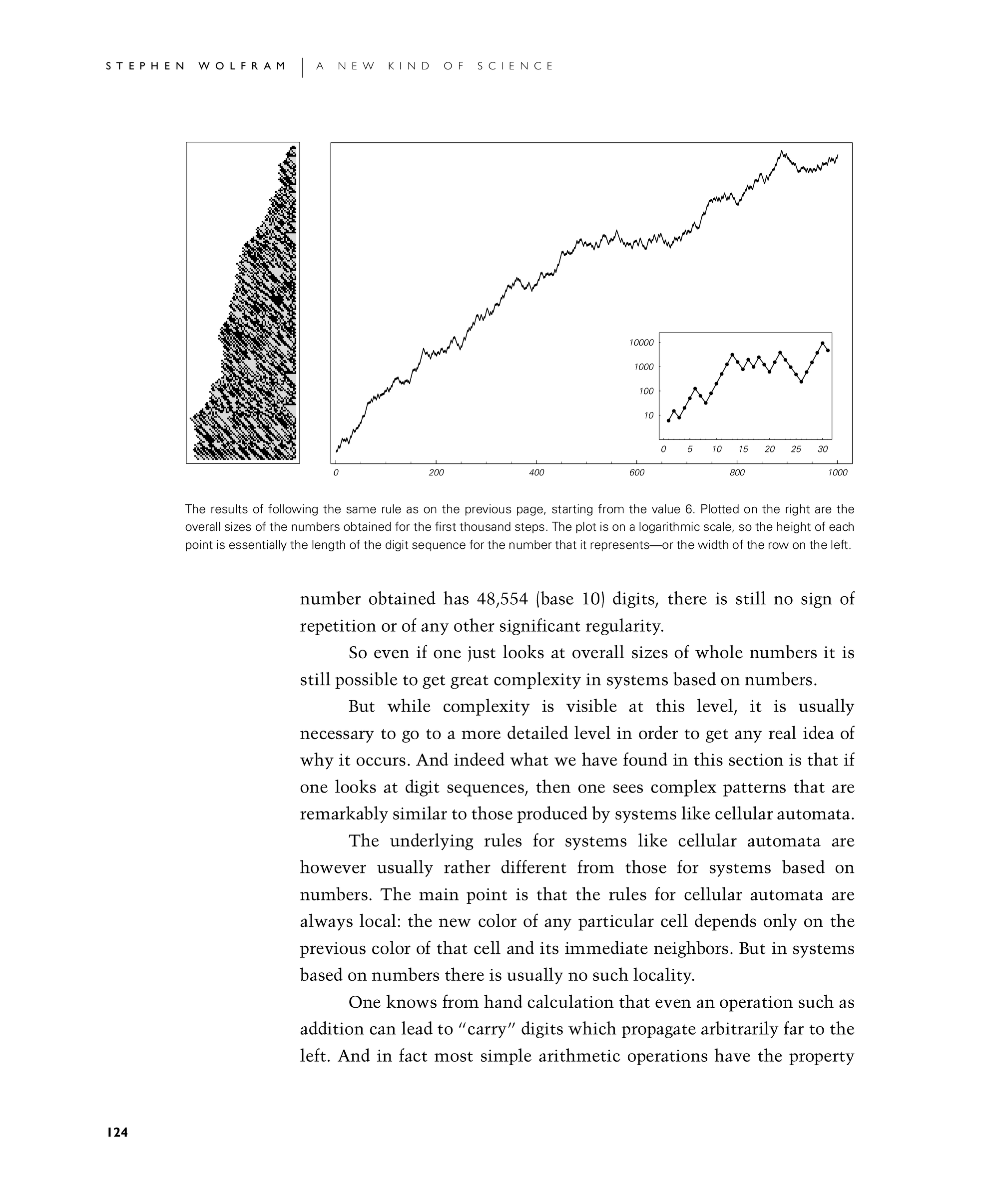
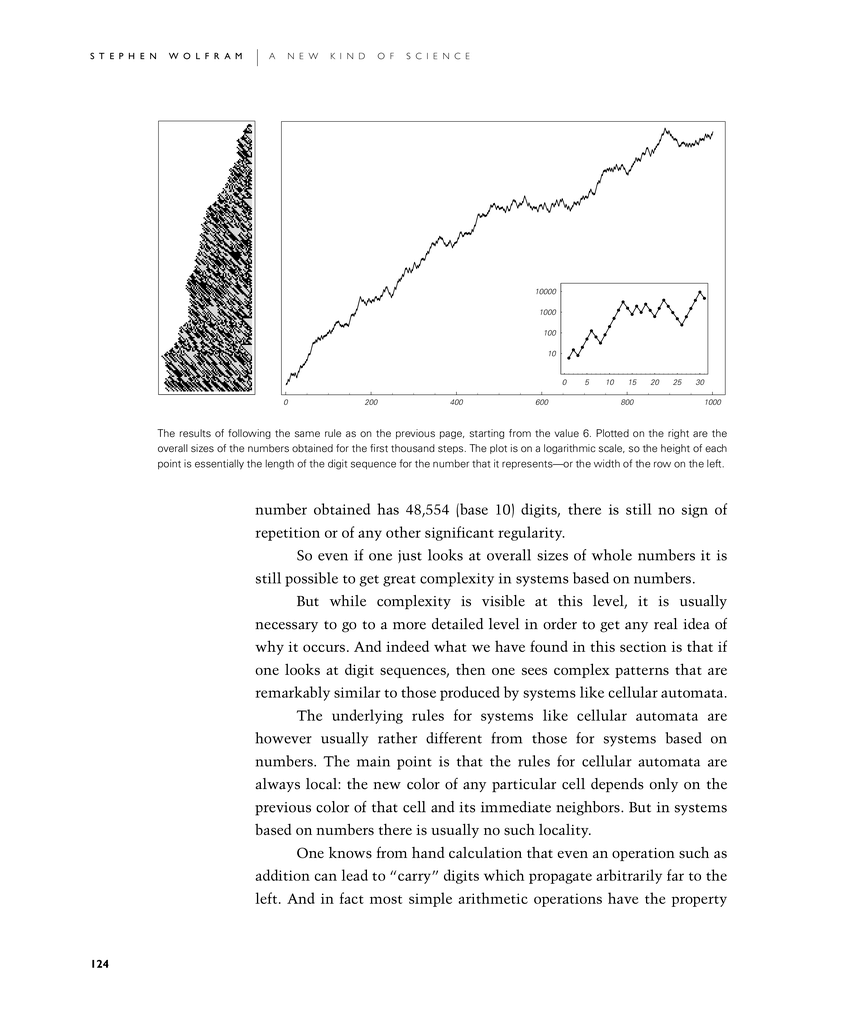
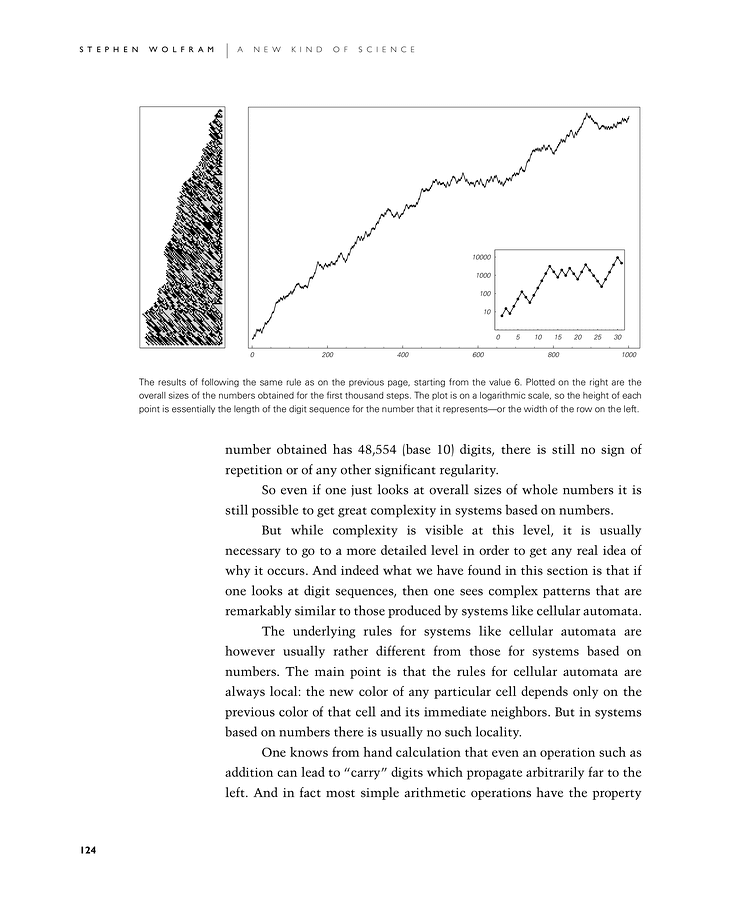
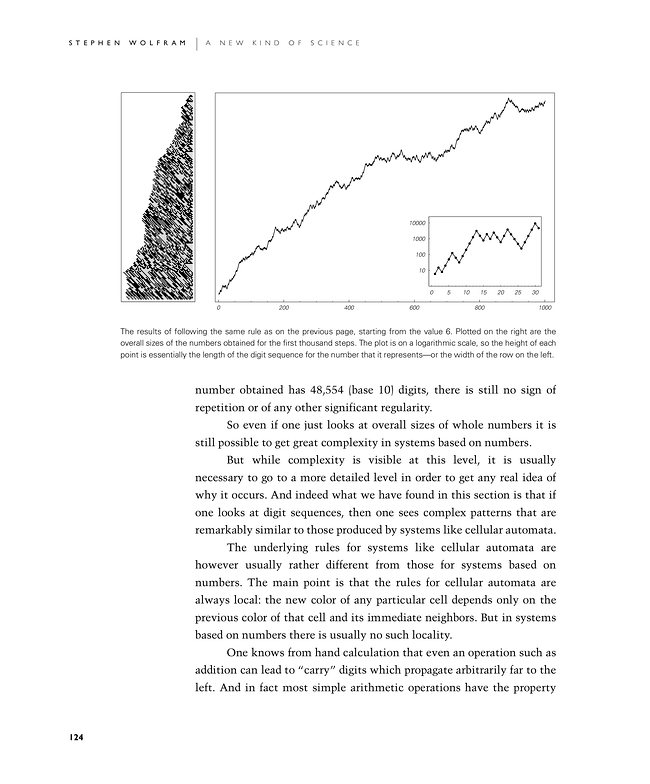
number obtained has 48,554 (base 10) digits, there is still no sign of repetition or of any other significant regularity.
So even if one just looks at overall sizes of whole numbers it is still possible to get great complexity in systems based on numbers.
But while complexity is visible at this level, it is usually necessary to go to a more detailed level in order to get any real idea of why it occurs. And indeed what we have found in this section is that if one looks at digit sequences, then one sees complex patterns that are remarkably similar to those produced by systems like cellular automata.
The underlying rules for systems like cellular automata are however usually rather different from those for systems based on numbers. The main point is that the rules for cellular automata are always local: the new color of any particular cell depends only on the previous color of that cell and its immediate neighbors. But in systems based on numbers there is usually no such locality.
One knows from hand calculation that even an operation such as addition can lead to "carry" digits which propagate arbitrarily far to the left. And in fact most simple arithmetic operations have the property
 |  |
The results of following the same rule as on the previous page, starting from the value 6. Plotted on the right are the overall sizes of the numbers obtained for the first thousand steps. The plot is on a logarithmic scale, so the height of each point is essentially the length of the digit sequence for the number that it represents—or the width of the row on the left.