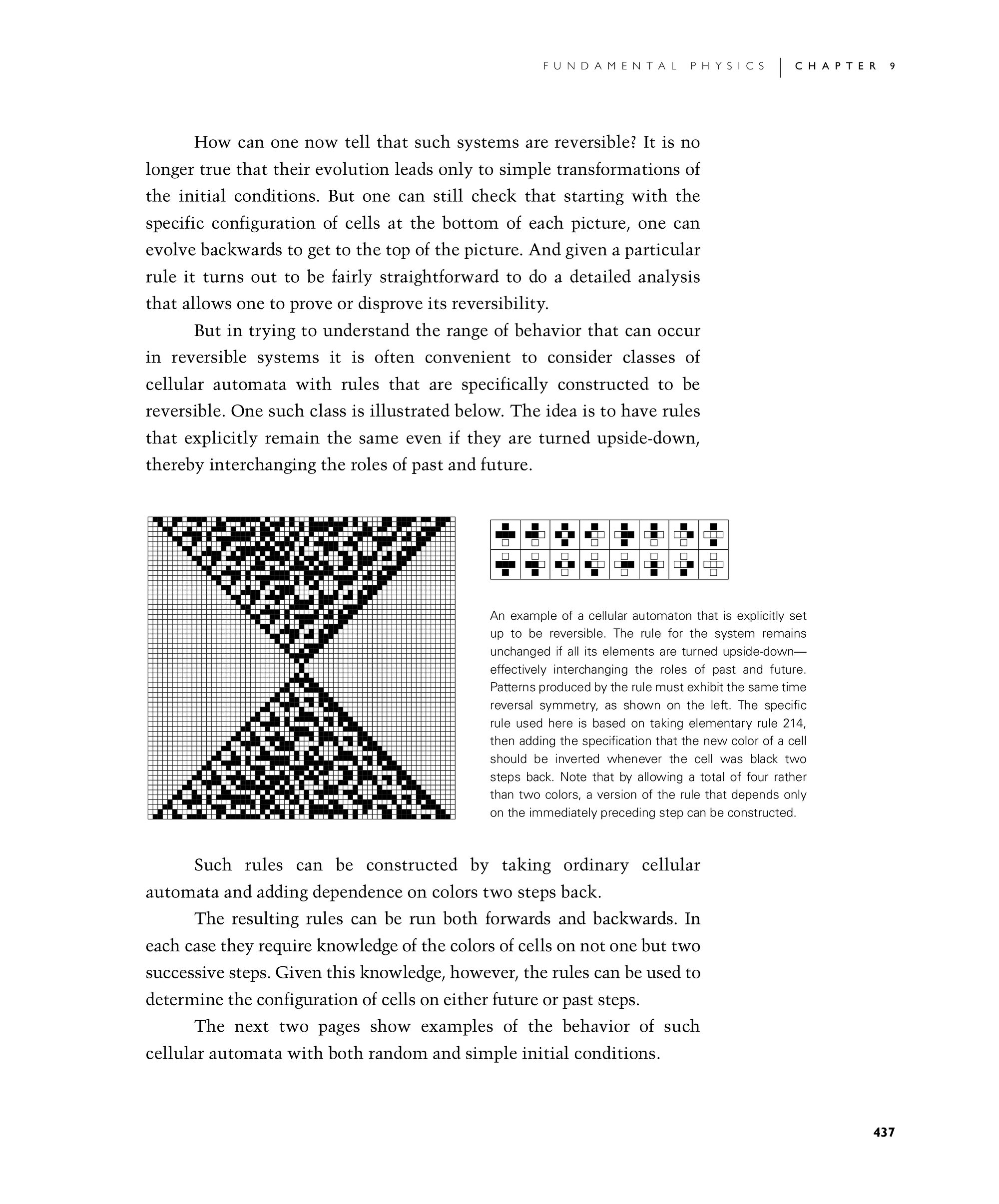
How can one now tell that such systems are reversible? It is no longer true that their evolution leads only to simple transformations of the initial conditions. But one can still check that starting with the specific configuration of cells at the bottom of each picture, one can evolve backwards to get to the top of the picture. And given a particular rule it turns out to be fairly straightforward to do a detailed analysis that allows one to prove or disprove its reversibility.

But in trying to understand the range of behavior that can occur in reversible systems it is often convenient to consider classes of cellular automata with rules that are specifically constructed to be reversible. One such class is illustrated below. The idea is to have rules that explicitly remain the same even if they are turned upside-down, thereby interchanging the roles of past and future.

Such rules can be constructed by taking ordinary cellular automata and adding dependence on colors two steps back.

The resulting rules can be run both forwards and backwards. In each case they require knowledge of the colors of cells on not one but two successive steps. Given this knowledge, however, the rules can be used to determine the configuration of cells on either future or past steps.

The next two pages [438, 439] show examples of the behavior of such cellular automata with both random and simple initial conditions.

An example of a cellular automaton that is explicitly set up to be reversible. The rule for the system remains unchanged if all its elements are turned upside-down—effectively interchanging the roles of past and future. Patterns produced by the rule must exhibit the same time reversal symmetry, as shown on the left. The specific rule used here is based on taking elementary rule 214, then adding the specification that the new color of a cell should be inverted whenever the cell was black two steps back. Note that by allowing a total of four rather than two colors, a version of the rule that depends only on the immediately preceding step can be constructed.