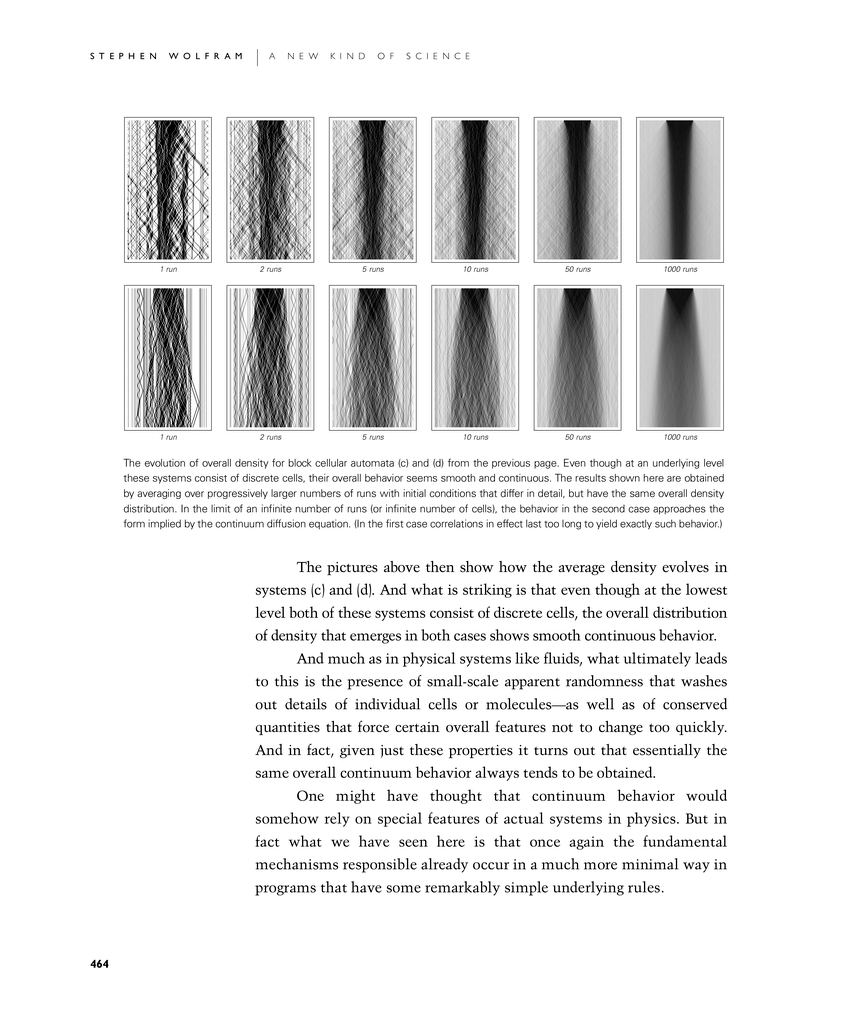
The pictures below then show how the average density evolves in systems (c) and (d). And what is striking is that even though at the lowest level both of these systems consist of discrete cells, the overall distribution of density that emerges in both cases shows smooth continuous behavior.

And much as in physical systems like fluids, what ultimately leads to this is the presence of small-scale apparent randomness that washes out details of individual cells or molecules—as well as of conserved quantities that force certain overall features not to change too quickly. And in fact, given just these properties it turns out that essentially the same overall continuum behavior always tends to be obtained.

One might have thought that continuum behavior would somehow rely on special features of actual systems in physics. But in fact what we have seen here is that once again the fundamental mechanisms responsible already occur in a much more minimal way in programs that have some remarkably simple underlying rules.

The evolution of overall density for block cellular automata (c) and (d) from the previous page. Even though at an underlying level these systems consist of discrete cells, their overall behavior seems smooth and continuous. The results shown here are obtained by averaging over progressively larger numbers of runs with initial conditions that differ in detail, but have the same overall density distribution. In the limit of an infinite number of runs (or infinite number of cells), the behavior in the second case approaches the form implied by the continuum diffusion equation. (In the first case correlations in effect last too long to yield exactly such behavior.)