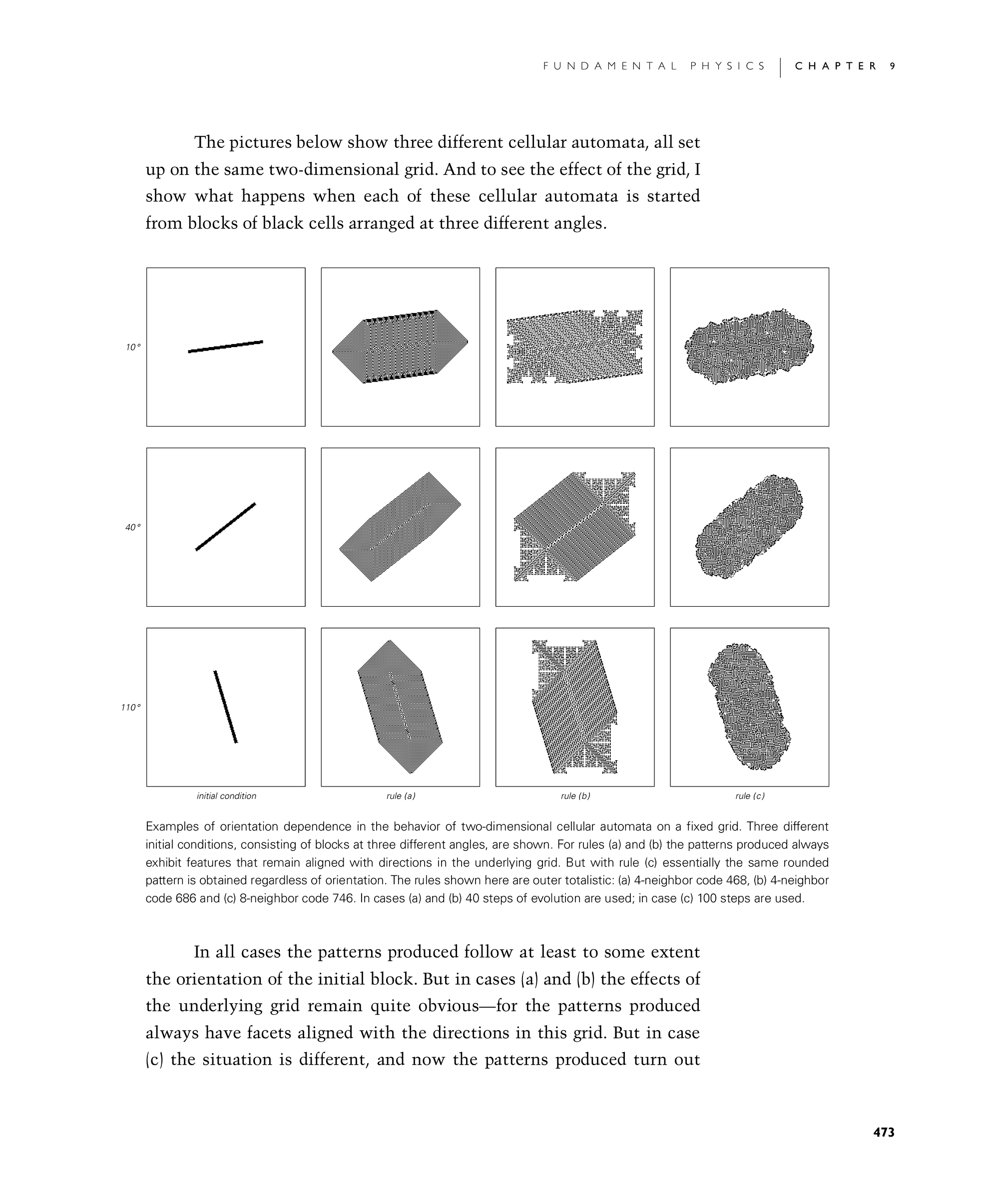
The pictures below show three different cellular automata, all set up on the same two-dimensional grid. And to see the effect of the grid, I show what happens when each of these cellular automata is started from blocks of black cells arranged at three different angles.
In all cases the patterns produced follow at least to some extent the orientation of the initial block. But in cases (a) and (b) the effects of the underlying grid remain quite obvious—for the patterns produced always have facets aligned with the directions in this grid. But in case (c) the situation is different, and now the patterns produced turn out

Examples of orientation dependence in the behavior of two-dimensional cellular automata on a fixed grid. Three different initial conditions, consisting of blocks at three different angles, are shown. For rules (a) and (b) the patterns produced always exhibit features that remain aligned with directions in the underlying grid. But with rule (c) essentially the same rounded pattern is obtained regardless of orientation. The rules shown here are outer totalistic: (a) 4-neighbor code 468, (b) 4-neighbor code 686 and (c) 8-neighbor code 746. In cases (a) and (b) 40 steps of evolution are used; in case (c) 100 steps are used.