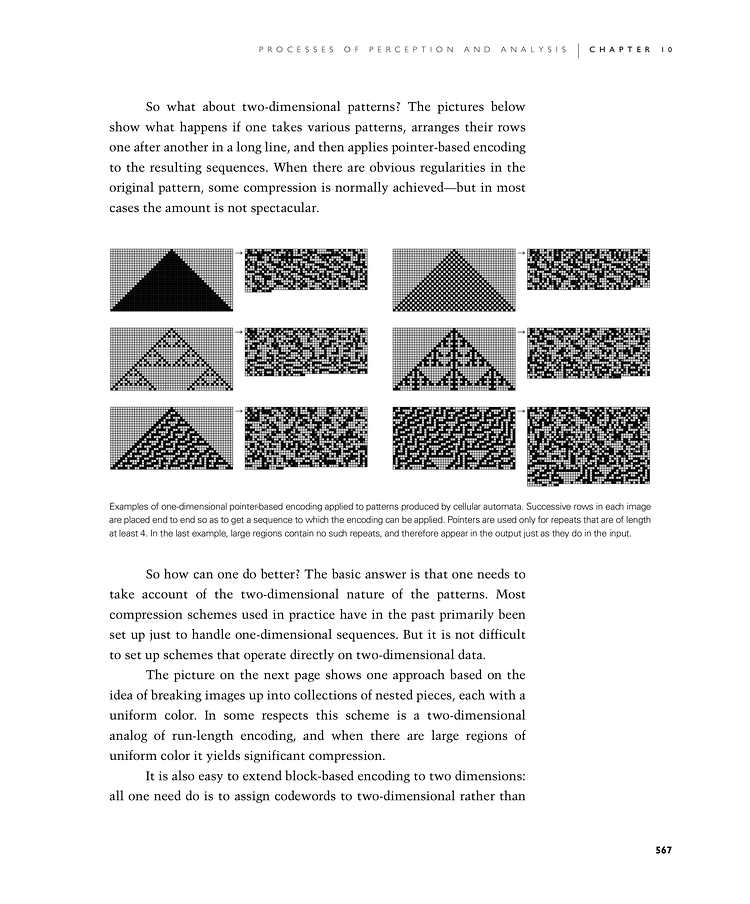
So what about two-dimensional patterns? The pictures below show what happens if one takes various patterns, arranges their rows one after another in a long line, and then applies pointer-based encoding to the resulting sequences. When there are obvious regularities in the original pattern, some compression is normally achieved—but in most cases the amount is not spectacular.
So how can one do better? The basic answer is that one needs to take account of the two-dimensional nature of the patterns. Most compression schemes used in practice have in the past primarily been set up just to handle one-dimensional sequences. But it is not difficult to set up schemes that operate directly on two-dimensional data.
The picture on the next page shows one approach based on the idea of breaking images up into collections of nested pieces, each with a uniform color. In some respects this scheme is a two-dimensional analog of run-length encoding, and when there are large regions of uniform color it yields significant compression.
It is also easy to extend block-based encoding to two dimensions: all one need do is to assign codewords to two-dimensional rather than

Examples of one-dimensional pointer-based encoding applied to patterns produced by cellular automata. Successive rows in each image are placed end to end so as to get a sequence to which the encoding can be applied. Pointers are used only for repeats that are of length at least 4. In the last example, large regions contain no such repeats, and therefore appear in the output just as they do in the input.