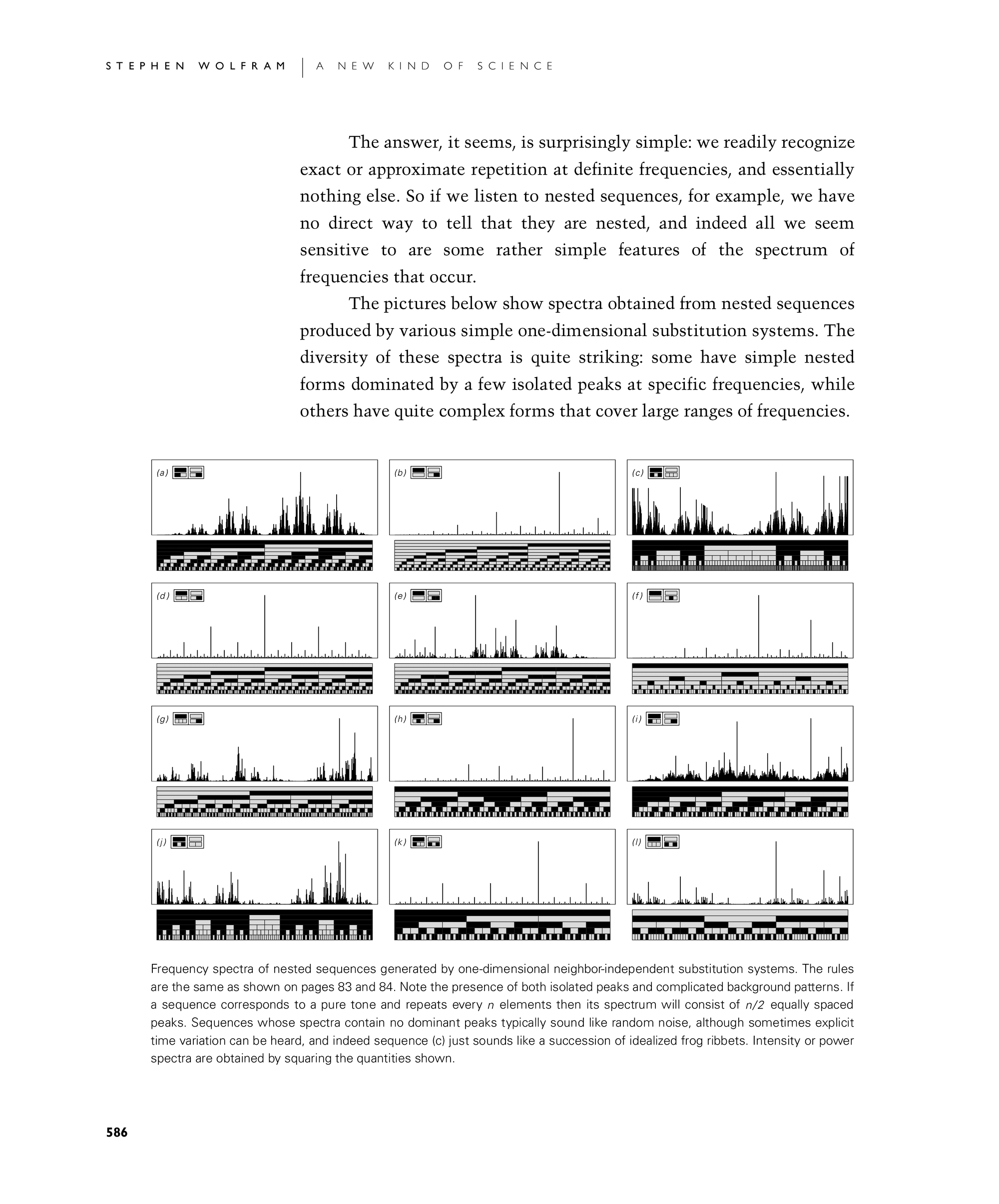
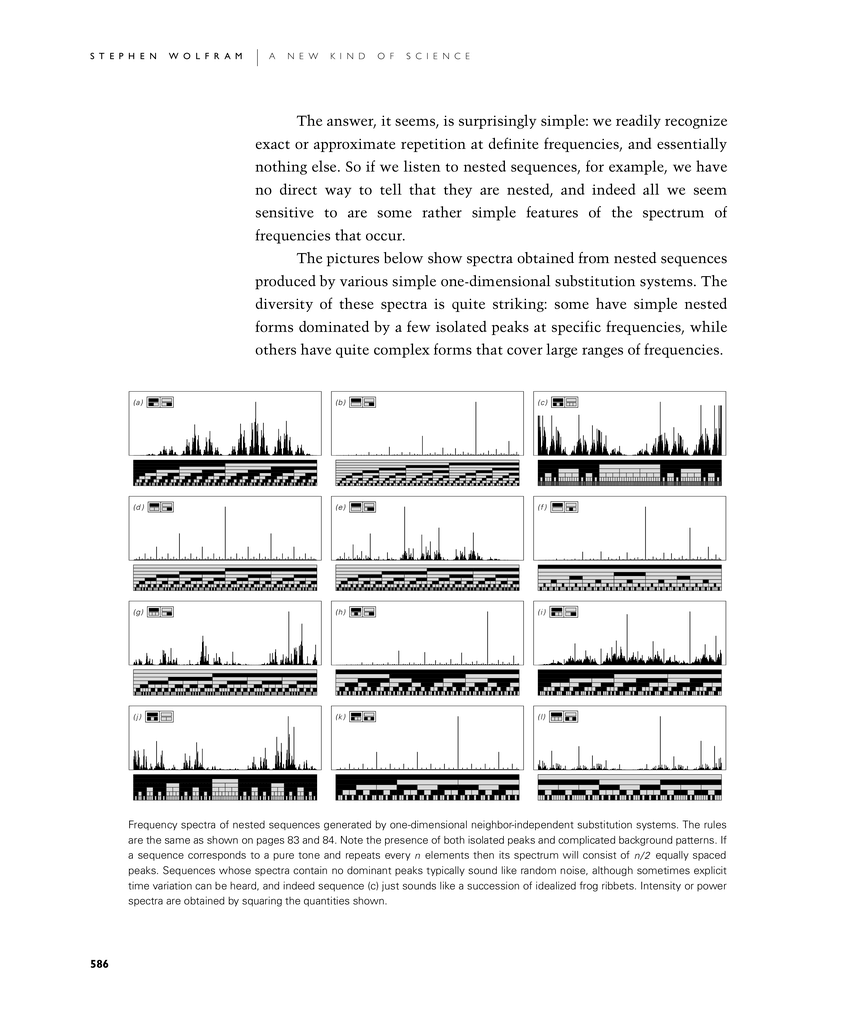
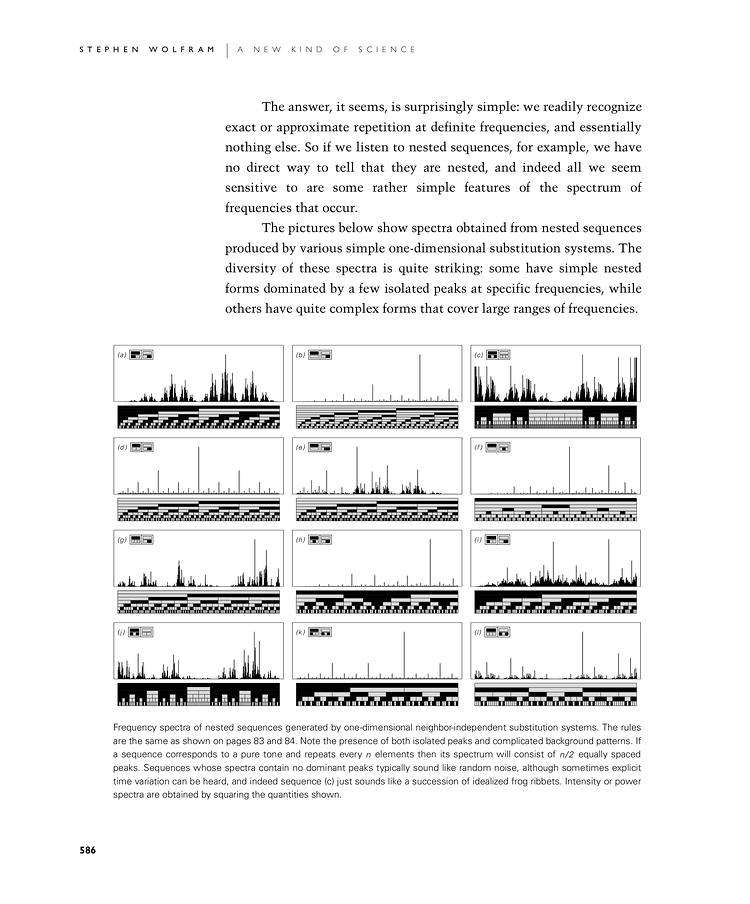
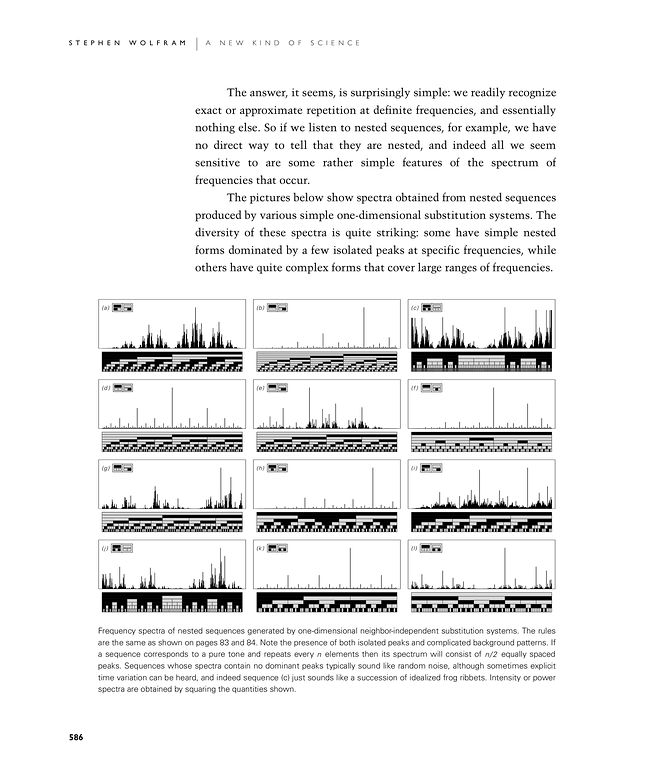
The answer, it seems, is surprisingly simple: we readily recognize exact or approximate repetition at definite frequencies, and essentially nothing else. So if we listen to nested sequences, for example, we have no direct way to tell that they are nested, and indeed all we seem sensitive to are some rather simple features of the spectrum of frequencies that occur.
The pictures below show spectra obtained from nested sequences produced by various simple one-dimensional substitution systems. The diversity of these spectra is quite striking: some have simple nested forms dominated by a few isolated peaks at specific frequencies, while others have quite complex forms that cover large ranges of frequencies.

Frequency spectra of nested sequences generated by one-dimensional neighbor-independent substitution systems. The rules are the same as shown on pages 83 and 84. Note the presence of both isolated peaks and complicated background patterns. If a sequence corresponds to a pure tone and repeats every n elements then its spectrum will consist of n/2 equally spaced peaks. Sequences whose spectra contain no dominant peaks typically sound like random noise, although sometimes explicit time variation can be heard, and indeed sequence (c) just sounds like a succession of idealized frog ribbets. Intensity or power spectra are obtained by squaring the quantities shown.