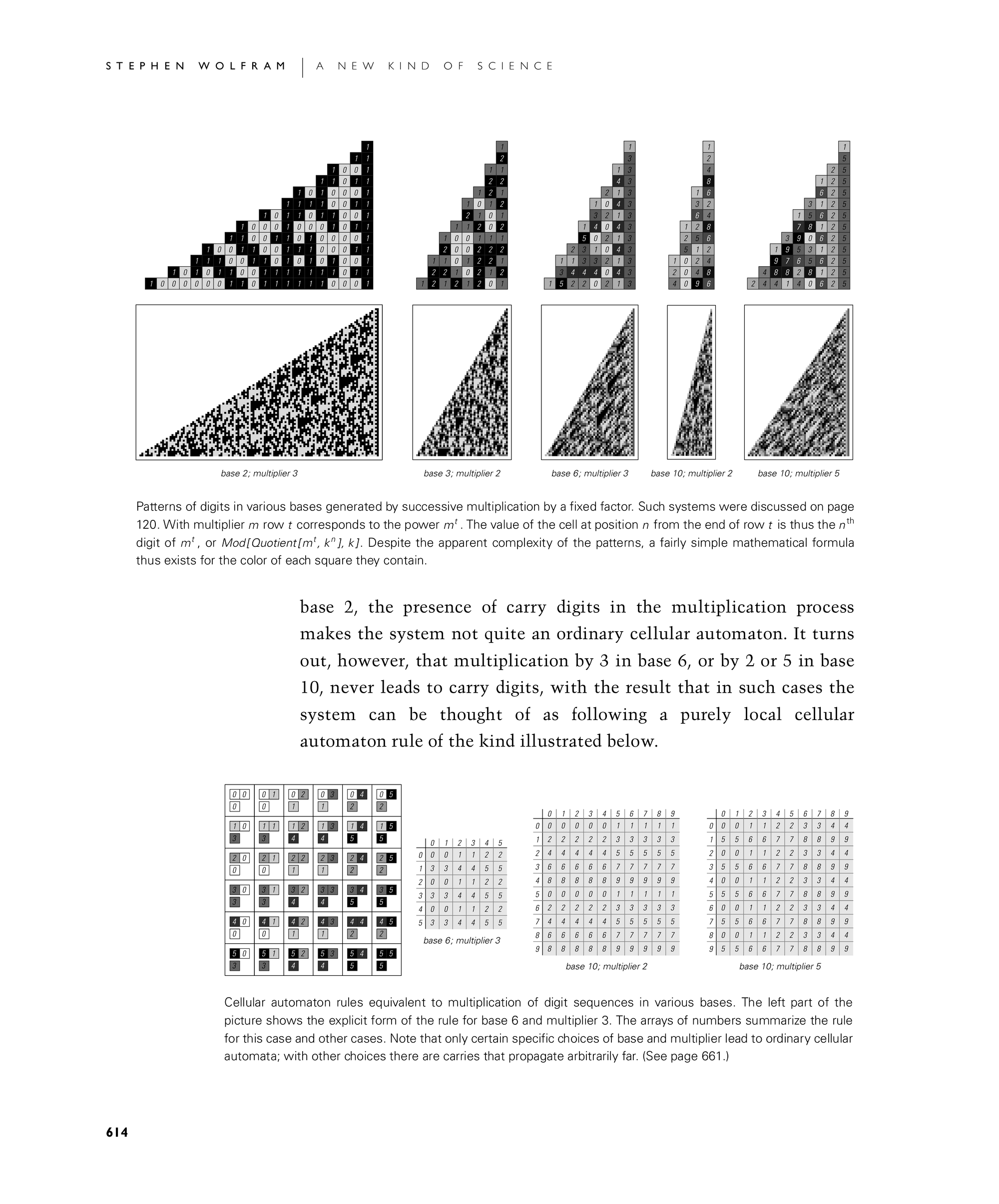
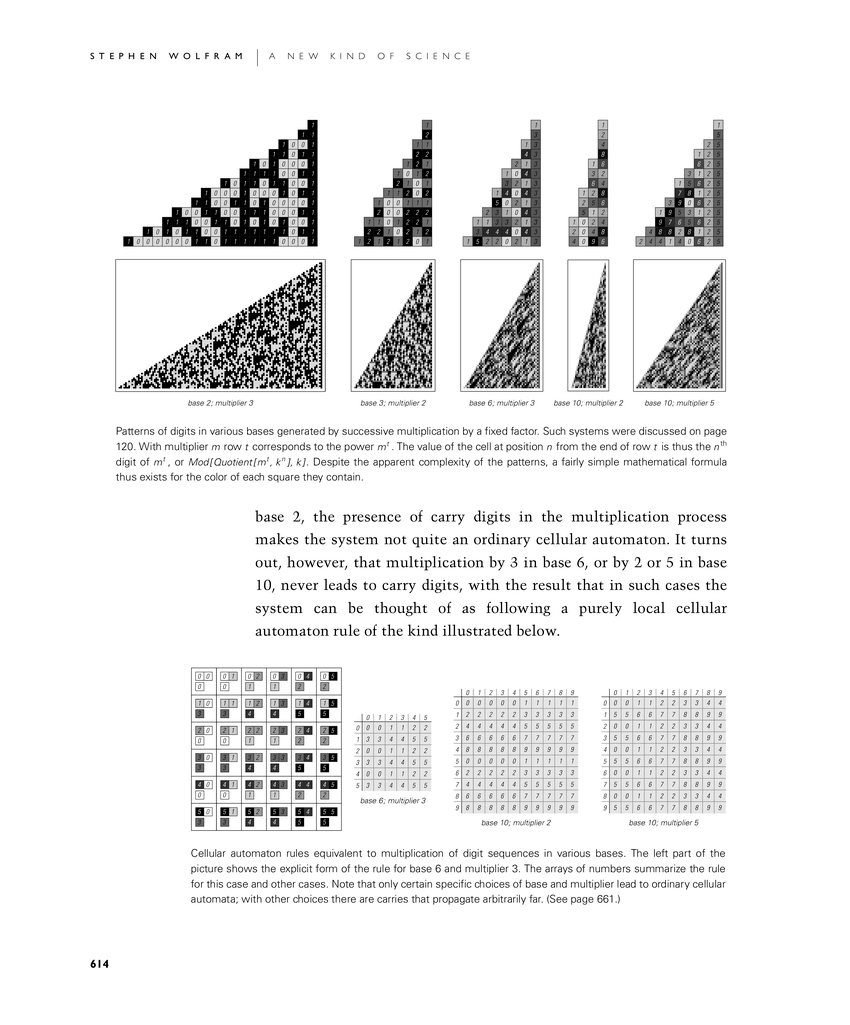
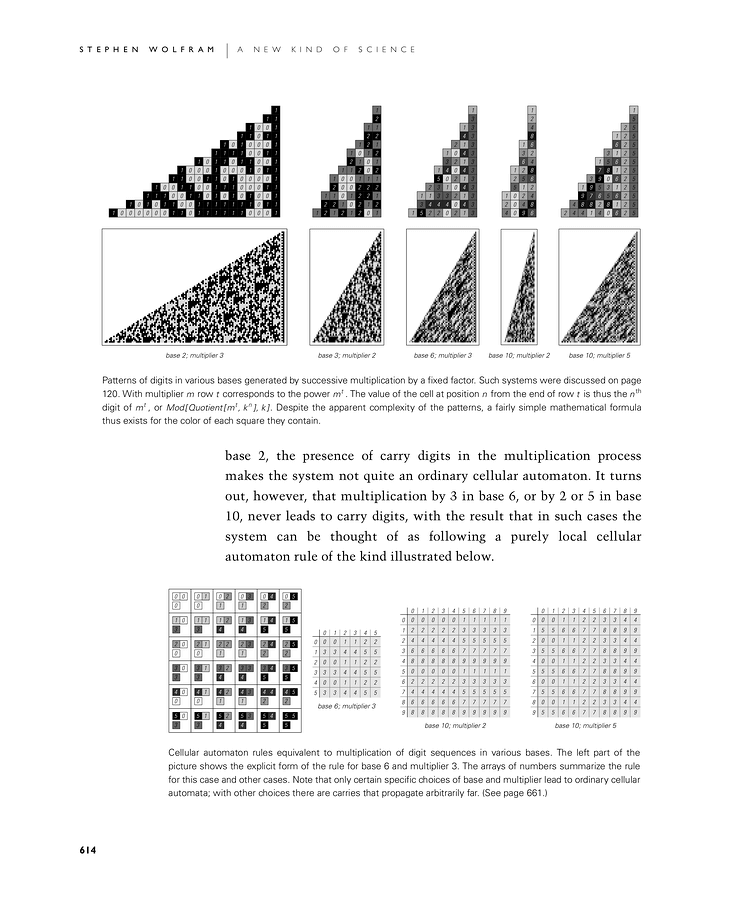
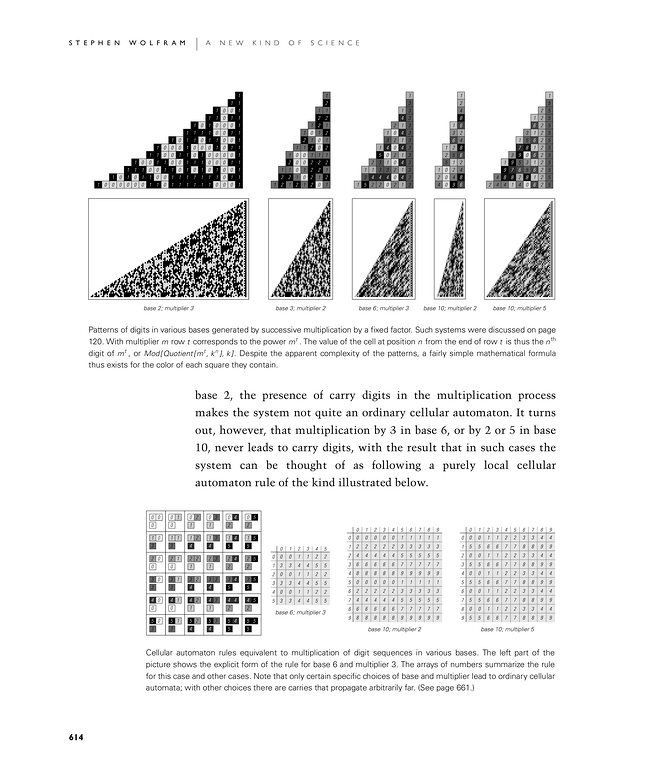
base 2, the presence of carry digits in the multiplication process makes the system not quite an ordinary cellular automaton. It turns out, however, that multiplication by 3 in base 6, or by 2 or 5 in base 10, never leads to carry digits, with the result that in such cases the system can be thought of as following a purely local cellular automaton rule of the kind illustrated in the second set of pictures.

Patterns of digits in various bases generated by successive multiplication by a fixed factor. Such systems were discussed on page 120. With multiplier m row t corresponds to the power mt. The value of the cell at position n from the end of row t is thus the nth digit of mt, or Mod[Quotient[mt, kn], k]. Despite the apparent complexity of the patterns, a fairly simple mathematical formula thus exists for the color of each square they contain.
 |  |  |
Cellular automaton rules equivalent to multiplication of digit sequences in various bases. The left part of the picture shows the explicit form of the rule for base 6 and multiplier 3. The arrays of numbers summarize the rule for this case and other cases. Note that only certain specific choices of base and multiplier lead to ordinary cellular automata; with other choices there are carries that propagate arbitrarily far. (See page 661.)