The pictures at the bottom of the facing page give examples of some 2-state 4-color Turing machines that show complex behavior. And I have little doubt that most if not all of these are universal.

Among such 2-state 4-color Turing machines perhaps one in 50,000 shows complex behavior when started from a blank tape. Among 4-state 2-color Turing machines the same kind of complex behavior is also seen—as discussed on page 81—but now it occurs only in perhaps one out of 200,000 cases.

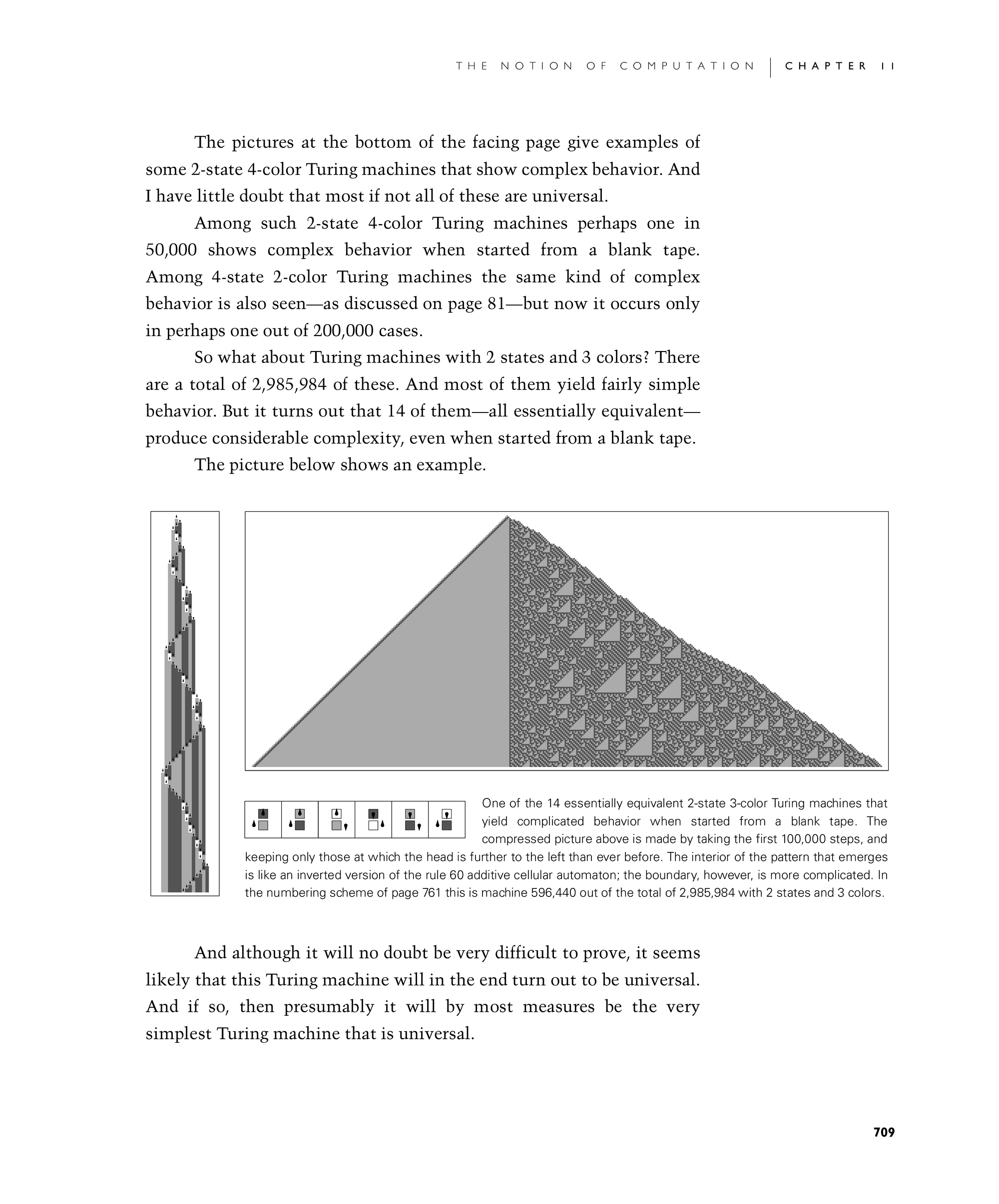
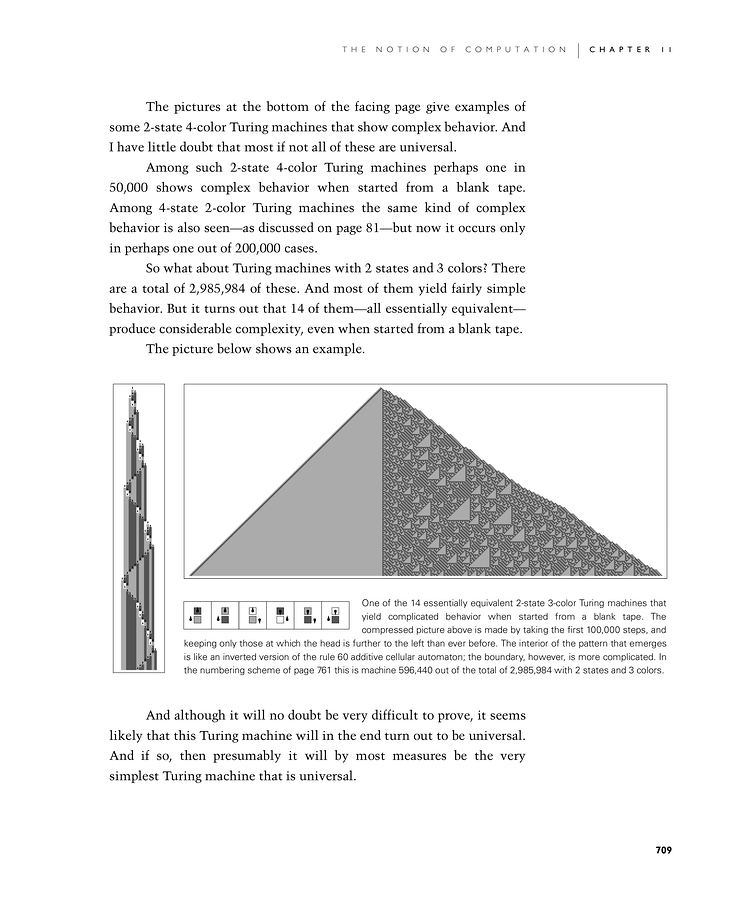
So what about Turing machines with 2 states and 3 colors? There are a total of 2,985,984 of these. And most of them yield fairly simple behavior. But it turns out that 14 of them—all essentially equivalent—produce considerable complexity, even when started from a blank tape.

The picture below shows an example.

And although it will no doubt be very difficult to prove, it seems likely that this Turing machine will in the end turn out to be universal. And if so, then presumably it will by most measures be the very simplest Turing machine that is universal.

One of the 14 essentially equivalent 2-state 3-color Turing machines that yield complicated behavior when started from a blank tape. The compressed picture above is made by taking the first 100,000 steps, and keeping only those at which the head is further to the left than ever before. The interior of the pattern that emerges is like an inverted version of the rule 60 additive cellular automaton; the boundary, however, is more complicated. In the numbering scheme of page 761 this is machine 596,440 out of the total of 2,985,984 with 2 states and 3 colors.