|
Complex Behavior in Digit Sequences Produced with Simple Iterated Maps
Christopher Maes
Massachusetts Institute of Technology
Iterated maps operating on 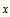 and the representation of and the representation of 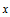 in base in base 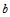 are studied. Particular attention is paid to the reversal addition map given by are studied. Particular attention is paid to the reversal addition map given by 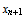 = = 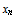 + R( + R(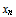 , , 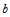 ) (where R( ) (where R(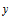 , , 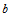 ) is the reversal of ) is the reversal of 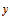 in base in base 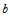 ). Qualitiative classes of behavior similar to those in cellular automata are found in successive terms in the sequence. An algorithm for classifying unique sequences and determining the behavior of a sequence is presented. All simple maps are enumerated and those maps which produce complex behavior are found. Carry propagation and dependence on initial conditions are analyzed. A conjecture on maps in the form f( ). Qualitiative classes of behavior similar to those in cellular automata are found in successive terms in the sequence. An algorithm for classifying unique sequences and determining the behavior of a sequence is presented. All simple maps are enumerated and those maps which produce complex behavior are found. Carry propagation and dependence on initial conditions are analyzed. A conjecture on maps in the form f(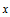 ) + R((g( ) + R((g(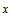 ), ), 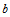 ) producing complex and thus universal behavior is presented. ) producing complex and thus universal behavior is presented.
Created by
Mathematica
(April 20, 2004)
|