|
Numbers as Programs
The Power of Digit Sequences
Eric Rowland
Rutgers University
Abstract
The base-b representation 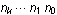 of a number n can be thought of as a list of instructions—a program—that generates n, in the sense that of a number n can be thought of as a list of instructions—a program—that generates n, in the sense that 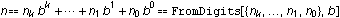 . It turns out that many other values associated with n can be computed by interpreting . It turns out that many other values associated with n can be computed by interpreting 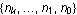 as a program in various ways. as a program in various ways.
The earliest (implicit) use of digit sequences as programs is likely the method of binary exponentiation known by Pingala in 200 BCE, in which the binary representation of n is used to efficiently compute 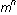 by repeated squaring. by repeated squaring.
Perhaps the first noteworthy explicit use came in 1852, when Kummer
discovered his famous result stating that the highest power to which a
prime p divides Binomial[n,m] is the
number of carries used when adding m and
n-m in base p.
There
have subsequently been several generalizations of this result, also
relying on digit sequences.
In the 1960s a theory emerged for automatic sequences, integer sequences in which the
nth term is produced by feeding
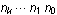 into a finite automaton.
(The Thue–Morse sequence is an example.) One drawback is that these
sequences necessarily take on only finitely many values. But
an important generalization of automatic sequences was provided by
Allouche and Shallit in 1992; this class of
k-regular
sequences includes sequences that take on infinitely many values, and this makes them useful for enumeration. For example, the two sequences beginning as follows are 2-regular. into a finite automaton.
(The Thue–Morse sequence is an example.) One drawback is that these
sequences necessarily take on only finitely many values. But
an important generalization of automatic sequences was provided by
Allouche and Shallit in 1992; this class of
k-regular
sequences includes sequences that take on infinitely many values, and this makes them useful for enumeration. For example, the two sequences beginning as follows are 2-regular.

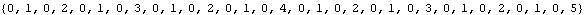
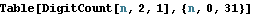
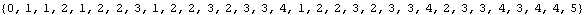
There is an analogous machine model for k-regular sequences, which makes them quick to compute. However, the underlying machine can be difficult to guess from experimental data.
I will discuss these examples of digit sequences as programs and others that have arisen in my own work on Pascal's triangle and additive cellular automata.
|