|
Novel Findings for Abelian Square Avoidance
Veikko Keränen
Rovaniemi Polytechnic, School of Technology
Abstract
An abelian square is a non-empty word of the form uv, where u and v are permutations, or anagrams, of each other. A word is called abelian square-free (a-2-free), if it does not contain any abelian square as a factor. The a-2-freeness property of words has been investigated since 1961, when Paul Erdös raised the question whether this kind of repetition can be avoided in words of arbitrary length. After extensive computer experiments, thirty years later, we found one a-2-free endomorphism 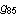 over a four-letter alphabet ( over a four-letter alphabet (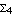 ). Until now, all known methods for constructing arbitrarily long a-2-free words over four letters have been based on the structure of this ). Until now, all known methods for constructing arbitrarily long a-2-free words over four letters have been based on the structure of this 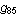 , or on the endomorphism , or on the endomorphism 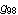 that we found some 11 years later. Actually, that we found some 11 years later. Actually, 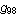 is not fully a-2-free although it can be used successfully in iterations. is not fully a-2-free although it can be used successfully in iterations.
After almost 17 years of search, it seemed quite impossible to find any more new examples of a-2-free endomorphisms of 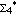 . Nevertheless, by using extensive distributed computation, we have recently succeeded in finding a great number of a-2-free endomorphisms of . Nevertheless, by using extensive distributed computation, we have recently succeeded in finding a great number of a-2-free endomorphisms of 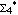 , with sizes from 4×102 to 4×115 (uniform modulus). , with sizes from 4×102 to 4×115 (uniform modulus).
More important is that some of the new a-2-free endomorphisms (with modulus 109) can be used to construct a powerful a-2-free substitution of 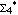 with 12 image words for each letter. The properties of this substitution improve significantly the preexisting lower bound for the exponential growth of the number of a-2-free words over four letters. The key characteristics of the new a-2-free substitution derive from delicate mutations in the image words. These mutations merely emerged from the computations. We do not think it would have been feasible to create them by any design. with 12 image words for each letter. The properties of this substitution improve significantly the preexisting lower bound for the exponential growth of the number of a-2-free words over four letters. The key characteristics of the new a-2-free substitution derive from delicate mutations in the image words. These mutations merely emerged from the computations. We do not think it would have been feasible to create them by any design.
Approaching the problem from the other direction, we are now able to explain, at least partly, the rareness of long words avoiding abelian squares by using the concept of an unfavorable factor. We take an abelian square-free word and, by using computers, try to extend it in an abelian square-free fashion alternately to the right and to the left with all possible ways up to a given upper bound for the total length. At a time, the length of the words increases only by a given fixed length. If the given upper bounds are reached then the original word is a so-far-favorable one (it may still turn out to be unfavorable on later experiments). If there is no way to reach the upper bounds, then the original word is classified, without any doubt, as unfavorable. Thus we obtain three kinds of words: unfavorable (bad), so-far-favorable (so-far-so-good), and favorable (good). It is a remarkable phenomenon that already relatively short so-far-favorable words turn out to be unfavorable factors after being "safely" extendable (to right and left) for quite a long distance and sometimes with a really huge number of branches. One of the most surprising behaviors is that of abcdacbabdabacdacbcdad. For this word of length 22, we obtain the following list of pairs (x, y), where x represents the length of the words in the so-far-favorable bidirectional tree, and y represents the number of all possible extensions of the length in question. Below the words are extended only by one letter at a time (all extensions of length 1 are tried). In a shortened form, the list is as follows:
{{22, 1}, {23, 2}, {24, 2}, {25, 5}, {26, 14}, {27, 23}, {28, 14}, {29, 26}, {30, 10}, {31, 16}, {32, 8}, {33, 9}, {34, 9}, {35, 16}, {36, 16}, {37, 27}, {38, 27}, {39, 54}, {40, 54}, {41, 68}, {42, 136}, {43, 194}, {44, 291}, {45, 444}, {46, 296}, {47, 450}, {48, 225}, {49, 331}, {50, 331}, {51, 474}, {52, 948}, ... , {107, 840479}, {108, 1679287}, {109, 2301836}, {110, 2302465}, {111, 3157227}, {112, 3154210}, {113, 4306159}, {114, 8466798}, {115, 11575001}, {116, 5779271}, {117, 7866918}, {118, 0}}.
The death of all nearly 8 million branches of this bidirectional tree at length 117 looks dramatic. We remark that it was necessary to construct all the possible a-2-free words in the tree to be able to find the numbers and see the collapse. Consequently, the computation is quite a big one, but of course an even more massive search was needed to find this example in the first place. In all our research, it has been crucial to distribute the computations. In these computations we have been using Mathematica extensively.
In a way, the experimental facts concerning unfavorable factors explain a highly nonlinear behavior of our earlier computations and also the difficulty of finding abelian square-free endomorphisms of 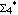 (not to speak of substitutions). At present we know that in the four-letter case about 60% of the abelian square-free words of length 24 are indeed unfavorable. (not to speak of substitutions). At present we know that in the four-letter case about 60% of the abelian square-free words of length 24 are indeed unfavorable.
|
 |

|