Technical Details

The Rules for the Machine

The rules for the Turing machine that is the subject of this prize are:

{{1, 2} -> {1, 1, -1}, {1, 1} -> {1, 2, -1}, {1, 0} -> {2, 1, 1},
{2, 2} -> {1, 0, 1}, {2, 1} -> {2, 2, 1}, {2, 0} -> {1, 2, -1}}

where this means {state, color} -> {state, color, offset}. (Colors of cells on the tape are sometimes instead thought of as "symbols" written to the tape.)

These rules can be represented pictorially by:

where the orientation of each arrow represents the state.

The rules can also be represented by the state transition diagram:

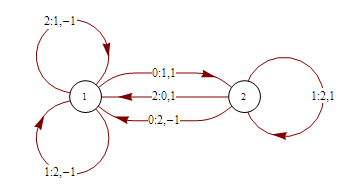
In Wolfram's numbering scheme for Turing machines, this is machine 596440. There are a total of (2 3 2)^(2 3)=12^6=2985984 machines with 2 states and 3 colors.

Note that there is no halt state for this Turing machine.

The machine operates on an infinite tape, as described in What is a Turing Machine?.

The machine can be implemented using the TuringMachine function in Mathematica. The evolution from a blank tape (and state 1) for 100 steps is given by:

TuringMachine[{596440, 2, 3}, {1, {{}, 0}}, 100]

What is Already Known

In the NKS book, Stephen Wolfram gives some results about the prize Turing machine in the main text on page 709 and in the Notes on page 1120.

A basic observation is that when the machine is in state 1, it operates on non-white cells by switching their color and moving to the left.

It is often convenient to study compressed versions of the evolution of the machine, though great care must be taken not to lose important information in the compression.

The pictures below show schemes for compression. The left-hand picture keeps only those steps at which the head is further to the left than it has ever been before ("left compression"). The right-hand picture keeps all steps at which the head changes direction.

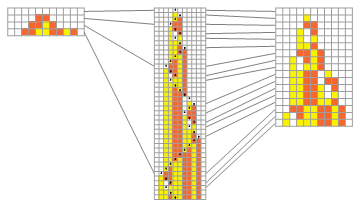
A notable result in the NKS book is that the "interior" of the left-compressed evolution of the machine from a finite region of non-white cells always follows the additive rule 60 cellular automaton. (There is a complete algebraic theory of rule 60, as discussed on pages 610 and 951 of the NKS book, and in an earlier paper.)

The NKS book gives a simple program for the left-compression evolution in the case of an initial condition with no "interior" white cells. Slightly rearranged, and using functions from Mathematica, the successive tape configurations for t steps of compressed evolution are given by:

1+NestList[(Join[{1}, Mod[Accumulate[#], 2], {{1}, {1, 0, 1}}[[1+Mod[Total[#], 2]]]])&, init-1, t]

The number of ordinary Turing machine steps corresponding to a particular left-compressed history h is given by:

2 Total[Flatten[Rest[h]]] + Length[Last[h]] - Length[First[h]] - 7 (Length[h] - 1)

The pictures below show the left-compressed evolution from a "blank" initial tape, containing only white cells.

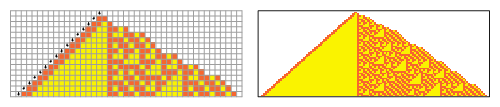
The left-hand side always expands by one cell at each compressed step. The right-hand side expands by either 1 or 3 cells.

The picture below shows the spacings between successive outward 3-cell jumps in 1000 steps of left-compressed evolution.

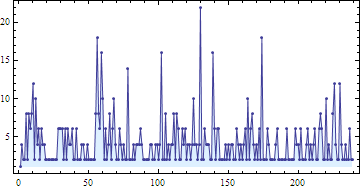
The behavior of the Turing machine is somewhat reminiscent of a tag system. It is also reminiscent of the classic 3n+1 unsolved problem in number theory.

The NKS book shows that questions about small Turing machines can quickly lead to elaborate number theory. A striking example is machine 600720 on page 1145. Note that even 2,2 Turing machines can already give rise to complex behavior with number theoretical features, as discussed on page 761 and in related notes.

For more information on what is already known, see the Gallery.

Related Turing Machines

There are 24 machines trivially related to machine 596440 by interchange of states, colors and directions. Note that complete equivalence of behavior can require transforming the initial conditions.

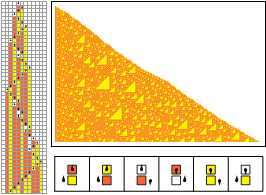
A closely related machine is 599870, as illustrated below. This machine has the same important features as 596440, but differs in some details. There are again 24 machines trivially related to 599870.

The Definition of Universality

Like many fundamental concepts, universality is in some ways clear and straightforward to define, and in other ways almost arbitrarily difficult to pin down. The general idea is that a system is universal if it can be "programmed" to emulate any other system. The difficulty comes in understanding what kinds of programming should be allowed. For if too much goes into the construction of the program, then computation can be done there, rather than in the system itself.

One common definition requires that the encoding of input for the universal system, and the decoding of its output, must both be done by a computation that always halts after a finite number of steps. One difficulty with this definition is that it may be too restrictive for infinite tapes. It is not clear, for instance, whether one should allow a Thue-Morse sequence in the initial conditions.

In most cases, it should nevertheless be fairly obvious whether something should be considered a valid encoding for a universal system. But in general there is no firmly established criterion. (For more information, see pages 722 and 1126 of the NKS book.)

For the purposes of this prize, the treatment of universality in any particular submission must be considered acceptable by the Prize Committee.

Proofs of Universality

The basic way that any current universality proof proceeds is by showing that the system to be proved universal can emulate all the behavior of some other system that is already known to be universal.

The proof can show emulation either of a specific universal system--such as the rule 110 cellular automaton--or of a whole class of systems that contain universal examples--such as all register machines.

In essence what the proof must do is to show that any initial conditions for the known universal system can be "encoded" as initial conditions for the system to be proved universal--and then that some aspect of the behavior of the system to be proved universal can be "decoded" to reproduce any given aspect of the known universal system.

Since the 1930s a few dozen general types of abstract systems have been proved universal, and a slightly smaller number of specific simple-to-describe systems have been proved universal. Essentially all practical computers and programming languages are also theoretically universal, at least if they are allowed unbounded memory.

Among general classes of systems known to be universal are Turing machines, register machines, recursive functions, tag systems, mobile automata, string rewriting (sequential substitution) systems, multiway systems, arithmetic systems and Diophantine equations.

Among specific systems known to be universal are Minsky's 7,4 Turing machine, Wolfram's 2,5 Turing machine, Conway's Game of Life cellular automaton, Wolfram's rule 110 cellular automaton, and Schonfinkel's S,K combinators.

Undecidability is closely related to universality. And while there are examples for which undecidability does not appear to imply universality, a proof of undecidability for some property of the prize Turing machine would be a significant step towards proving universality.

Note that the presence of universality implies that a particular system can emulate all other universal systems. But it does not necessarily imply that such emulation is efficient, say polynomial time.

Proofs of Non-Universality

It is less common to talk of "proving non-universality" than to talk of proving universality. To show that a system is not universal, one must show that no aspect of the system is capable of emulating a universal system.

One way to do this is to show that every aspect of the behavior of the system can be computed quickly using what amounts to a traditional "closed form" mathematical formula (and not an equation, iteration or procedure). This will always be the case if, for example, the system can show only repetitive or nested behavior.

Another way to show non-universality is to prove that every detail of the system can be reproduced by a simple translation from a system that is already known not to be universal--such as an additive cellular automaton like rule 60.

Still another way to show non-universality would be to establish that the system simply cannot compute some function that is known to be computable by a universal system. (An example of this general approach in a simpler situation is the proof that the Ackermann function cannot be primitive recursive.)

Much more common than discussing proofs of non-universality is discussing proofs of decidability.

There are many aspects of the prize Turing machine that can immediately be seen to be decidable. For example, the machine never halts, since it has no halt state. And given a finite initial condition (at least with no internal white cells), it is immediately decidable that the head for the machine will eventually go arbitrarily far to both the left and the right.

But there are many other questions about the prize Turing machine for which decidability is not immediately clear. To show that all possible questions enumerated in some way are decidable would in effect prove that the machine is not universal.

Another approach to proving non-universality would be to show that with all possible initial conditions, there is not enough variety in the patterns of behavior for the machine for it to be possible to represent an arbitrary computation. This would be the case if, for example, patterns for every different initial condition could be obtained by a simple transformation from the pattern for a blank initial condition.

Uses of the Term Universality

In this prize, the term "universality" is used in the sense of "computational universality" or "Turing completeness".

One technical point that should be clarified is the following. In the study of Turing machines with halting states, a universal Turing machine is sometimes defined to be one whose halting problem is r.e.-complete, which means that there is no decision procedure that tells whether the Turing machine will reach its halting state and that the language the Turing machine accepts can encode all other computable (recursively enumerable) languages. This notion of universality is useful from a theoretical point of view, but is not precisely the same as the one used in this prize. The prize Turing machine does not have a halt state, and to show universality for it, one must demonstrate that it can support arbitrary unbounded computations.

The term "universality" shows up in various contexts not directly equivalent to the computation universality considered in this prize. One important case is Boolean logic--in which any finite computation can be encoded (for example with Nand gates), but which cannot support the unbounded computations considered for Turing machines, or in this prize.

The "universality" discussed in the study of critical phenomena in statistical mechanics is not directly related to the computational universality of this prize. Nor is the "universality" sometimes discussed in the context of general philosophy.

Undecidability of Universality

While it is most likely that the prize Turing machine can either definitively be proved universal, or definitively be proved not universal, there is a strange intermediate possibility.

Just as in Godel's theorem, it could be that the question of whether the Turing machine is universal is independent of the standard axioms used in mathematics--say the axioms of Peano Arithmetic or of Zermelo-Fraenkel set theory.

At present, no specific problem as simple as the universality of the 2,3 Turing machine is known to be independent of standard axioms in this sense.

In some situations, showing that a statement is independent of the standard axioms immediately implies either that the statement is true, or that it is not true. But this is not the case for typical statements about universality.

Bibliography

The following lists some general and specific works relevant to the prize. For a more complete list of references, see the references contained in these works.

There is a large amount of relevant material in A New Kind of Science.

The papers below by Delvenne,Kůrka,Blondel and Sutner contain recent attempts to formalize the concept of universality for ongoing computational systems.

Blum, L., F. Cucker, M. Shub, and S. Smale. Complexity and Real Computation. Springer, 1997. [online version]

Chaitin, G. "Foundations of Mathematics." arXiv:math.HO/0203002v2 (2002). [online version]

Chaitin, G. Meta Math! The Quest for Omega. Atlantic Books, 2004. [online version]

Davis, M. Computability and Unsolvability. Dover Publications, 1985. [online version]

Davis, M. (Ed.) The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems and Computable Functions. Dover Publications, 2004. [online version]

Davis, M. The Universal Computer: The Road from Leibniz to Turing. W. W. Norton & Company, 2000. [online version]

Delvenne, J.-C., P. Kůrka, and V. Blondel. "Computational Universality in Symbolic Dynamical Systems." Lecture Notes in Computer Science: Machines, Computations, and Universality: 4th International Conference, MCU 3354 (2005): 104-115. [online version]

Herken, R. The Universal Turing Machine: A Half-Century Survey. Springer Verlag, 1995.

Kleene, S. Introduction to Metamathematics, North-Holland Publishing Company, 1952.

Margenstern, M. "Frontier between Decidability and Undecidability: A Survey." Theoretical Computer Science 231, no. 2 (2000): 217-251.

Matiyasevich, Yu. Hilbert's 10th Problem. MIT Press, 1993. [online version]

Minsky, M. Computation: Finite and Infinite Machines. Prentice-Hall, Inc., 1967.

Minsky, M. "Recursive Unsolvability of Post's Problem of 'Tag' and Other Topics in Theory of Turing Machines." Annals of Mathematics 74, no. 3 (1961): 437-453. [online version]

Post, E. "Finite Combinatory Processes--Formulation 1." Journal of Symbolic Logic 1, no. 3 (1936): 103-105. [online version]

Post, E. "Recursive Unsolvability of a Problem of Thue." Journal of Symbolic Logic 12, no. 3 (1947): 1-11. [online version]

Rogozhin, Yu. "Small Universal Turing Machines." Theoretical Computer Science 168, no. 2 (1996): 215-240.

Shannon, C. "A Universal Turing Machine with Two Internal States." Automata Studies. Princeton University Press (1956): 157-165. [online version]

Sutner, K. "Cellular Automata and Intermediate Degrees." Poster presented at NKS 2004. [online version]

Sutner, K. "Universality and Cellular Automata." In Lecture Notes in Computer Science: Machines, Computations, and Universality: 4th International Conference, MCU 3354 (2005): 50-59. [online version]

Turing, A. "On Computable Numbers, with an Application to the Entscheidungsproblem." Proceedings of the London Mathematical Society Series 2, 42 (1937): 230-265. [online version]

Turing, A. "On Computable Numbers, with an Application to the Entscheidungsproblem. A Correction." Proceedings of the London Mathematical Society Series 2, 43 (1938): 544-546. [online version]

Wolfram, S. A New Kind of Science. Wolfram Media, 2002. [online version]