Recursive Sequences
In the previous section, we saw that it is possible to get behavior of considerable complexity just by applying a variety of operations based on simple arithmetic. In this section what I will show is that with the appropriate setup just addition and subtraction turn out to be in a sense the only operations that one needs.
The basic idea is to consider a sequence of numbers in which there is a definite rule for getting the next number in the sequence from previous ones. It is convenient to refer to the first number in each sequence as f[1], the second as f[2], and so on, so that the nth number is denoted f[n]. And with this notation, what the rule does is to specify how f[n] should be calculated from previous numbers in the sequence.
In the simplest cases, f[n] depends only on the number immediately before it in the sequence, denoted f[n – 1]. But it is also possible to set up rules in which f[n] depends not only on f[n – 1], but also on f[n – 2], as well as on numbers still earlier in the sequence.
The table below gives results obtained with a few specific rules. In all the cases shown, these results are quite simple, consisting of sequences that increase uniformly or fluctuate in a purely repetitive way.
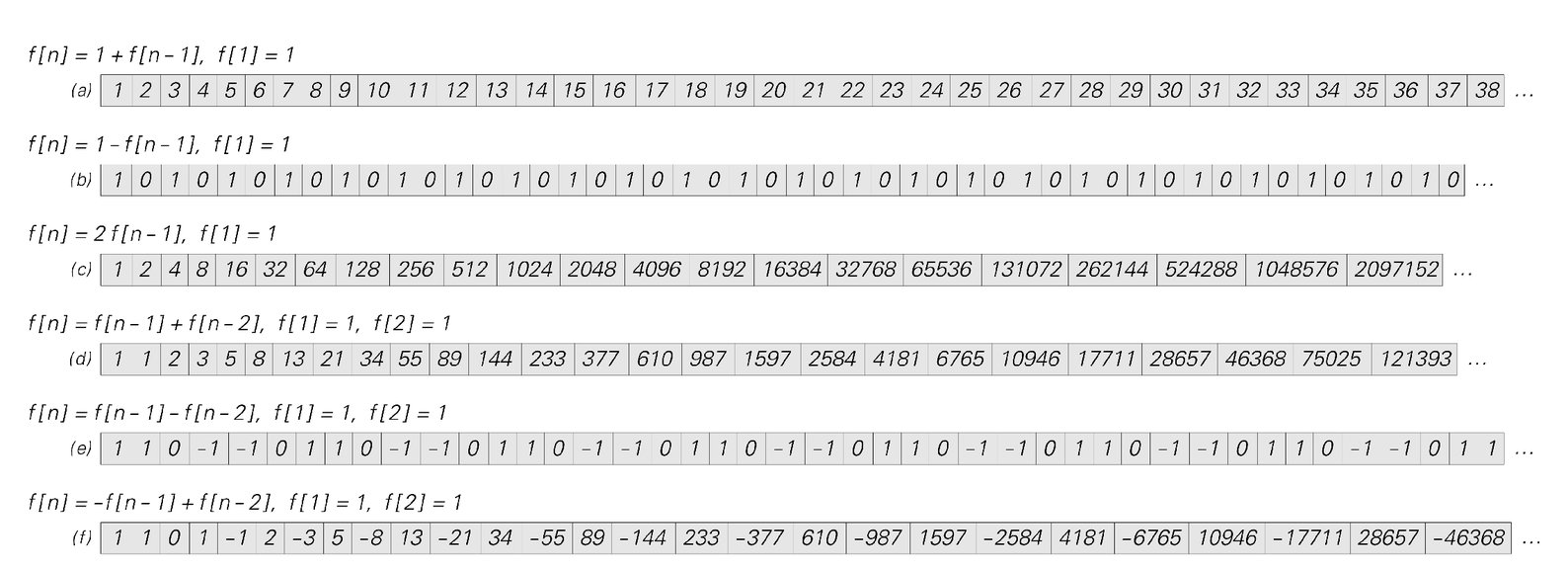
Examples of some simple recursive sequences. The nth element in each sequence is denoted f[n], and the rule specifies how this element is determined from previous ones. With all the rules shown here, successive elements either increase smoothly or fluctuate in a purely repetitive way. Sequence (c) is the powers of two; (d) is the so-called Fibonacci sequence, related to powers of the golden ratio (1 + √



