Data Compression
One usually thinks of perception and analysis as being done mainly in order to provide material for direct human consumption. But in most modern computer and communications systems there are processes equivalent to perception and analysis that happen all the time when data is compressed for more efficient storage or transmission.
One simple example of such a process is run-length encoding—a method widely used in practice to compress data that involves long sequences of identical elements, such as bitmap images of pages of text with large areas of white.
The basic idea of run-length encoding is to break data into runs of identical elements, and then to specify the data just by giving the lengths of these runs. This means, for example, that instead of having to list explicitly all the cells in a run of, say, 53 identical cells, one instead just gives the number "53". And the point is that even if the "53" is itself represented in terms of black and white cells, this representation can be much shorter than 53 cells.
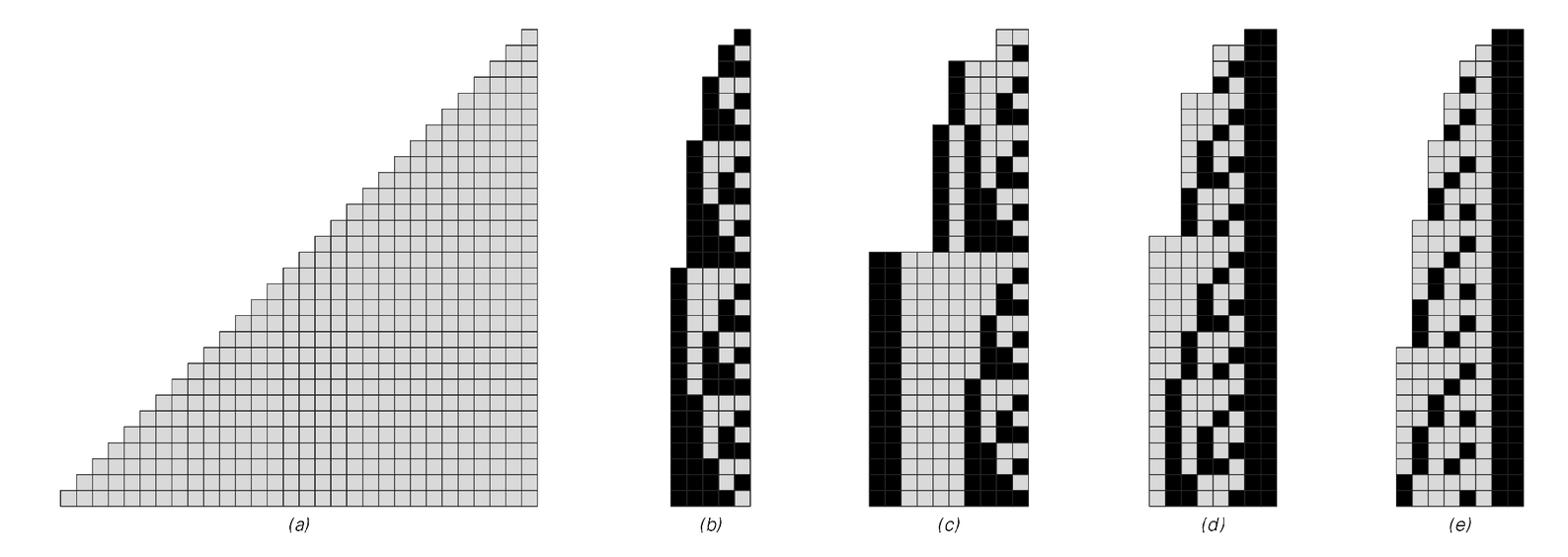
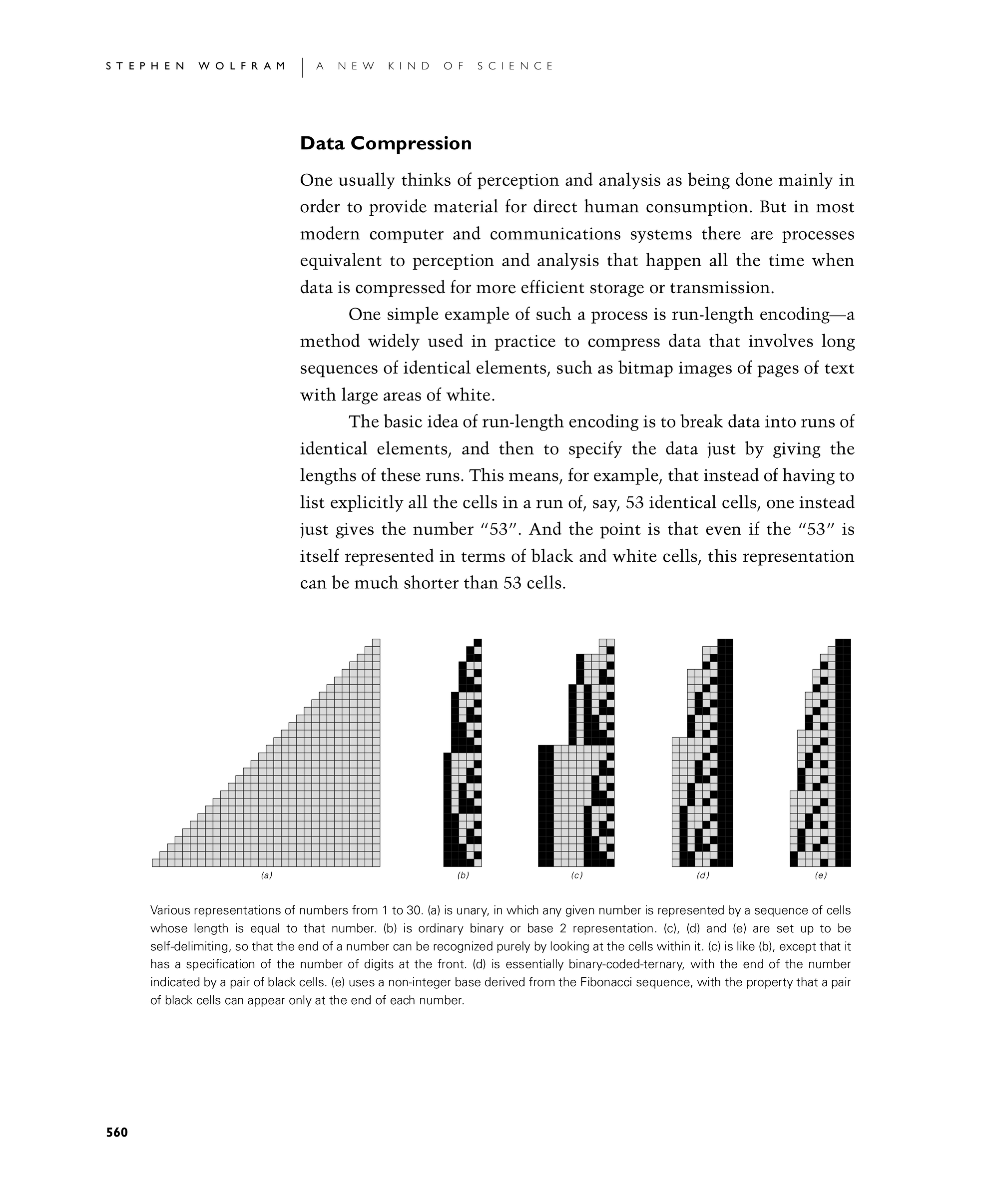
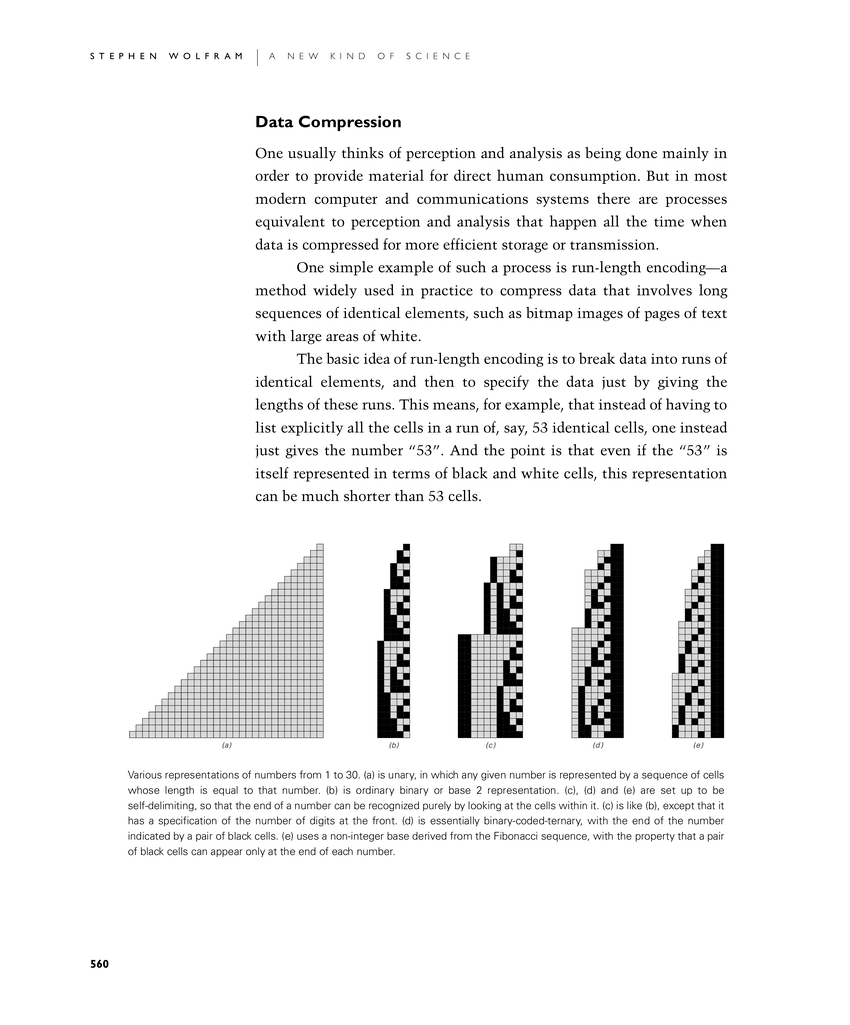
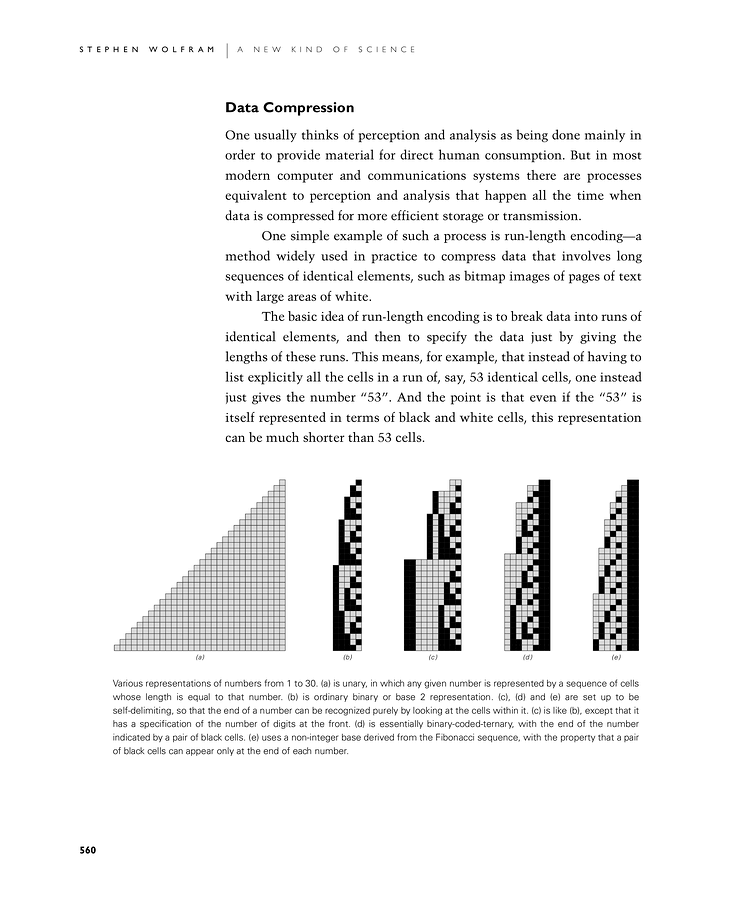
Various representations of numbers from 1 to 30. (a) is unary, in which any given number is represented by a sequence of cells whose length is equal to that number. (b) is ordinary binary or base 2 representation. (c), (d) and (e) are set up to be self-delimiting, so that the end of a number can be recognized purely by looking at the cells within it. (c) is like (b), except that it has a specification of the number of digits at the front. (d) is essentially binary-coded-ternary, with the end of the number indicated by a pair of black cells. (e) uses a non-integer base derived from the Fibonacci sequence, with the property that a pair of black cells can appear only at the end of each number.