Substitution Systems
One of the features that cellular automata, mobile automata and Turing machines all have in common is that at the lowest level they consist of a fixed array of cells. And this means that while the colors of these cells can be updated according to a wide range of different possible rules, the underlying number and organization of cells always stays the same.
Substitution systems, however, are set up so that the number of elements can change. In the typical case illustrated below, one has a sequence of elements—each colored say black or white—and at each step each one of these elements is replaced by a new block of elements.
In the simple cases shown, the rules specify that each element of a particular color should be replaced by a fixed block of new elements, independent of the colors of any neighboring elements.
And with these kinds of rules, the total number of elements typically grows very rapidly, so that pictures like those below quickly become rather unwieldy. But at least for these kinds of rules, one can make clearer pictures by thinking of each step not as replacing every element by a sequence of elements that are drawn the same size, but rather of subdividing each element into several that are drawn smaller.
In the cases on the facing page, I start from a single element represented by a long box going all the way across the picture. Then on successive steps the rules for the substitution system specify how each box should be subdivided into a sequence of shorter and shorter boxes.
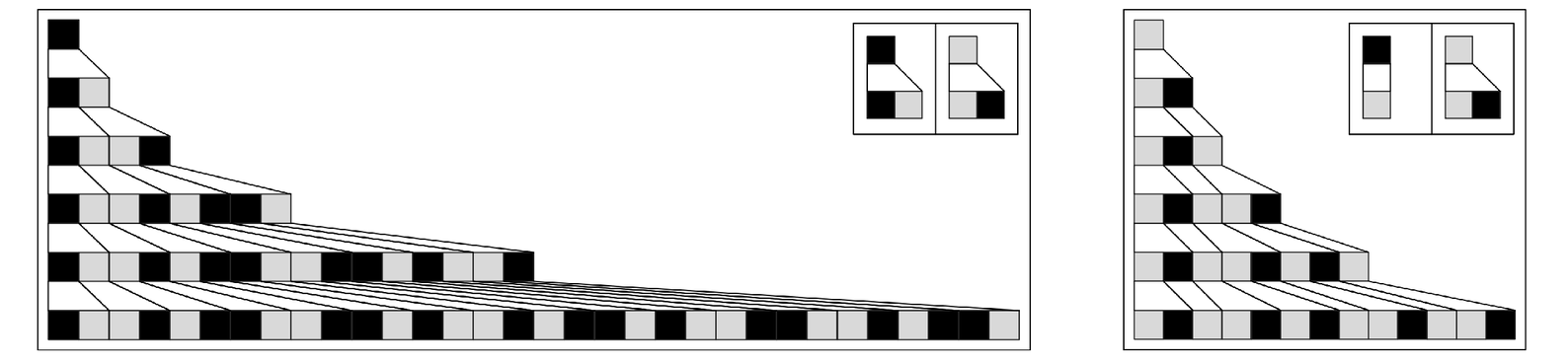
Examples of substitution systems with two possible kinds of elements, in which at every step each kind of element is replaced by a fixed block of new elements. In the first case shown, the total number of elements obtained doubles at every step; in the second case, it follows a Fibonacci sequence, and increases by a factor of roughly (1+Sqrt[5])/2 ≃ 1.618 at every step. The two substitution systems shown here correspond to the second and third examples in the pictures on the following two pages [83, 84].



