More Cellular Automata
The first picture below shows the rules used in the four cellular automata on the facing page. The overall structure of these rules is the same in each case; what differs is the specific choice of new colors for each possible combination of previous colors for a cell and its two neighbors.
There turn out to be a total of 256 possible sets of choices that can be made. And following my original work on cellular automata these choices can be numbered from 0 to 255, as in the second picture below.
But so how do cellular automata with all these different rules behave? The next page shows a few examples in detail, while the following two pages [55, 56] show what happens in all 256 possible cases.
At first, the diversity of what one sees is a little overwhelming. But on closer investigation, definite themes begin to emerge.
In the very simplest cases, all the cells in the cellular automaton end up just having the same color after one step. Thus, for example, in

The rules used for the four examples of cellular automata on the facing page. In each case, these specify the new color of a cell for each possible combination of colors of that cell and its immediate neighbors on the previous step. The rules are numbered according to the scheme described above.
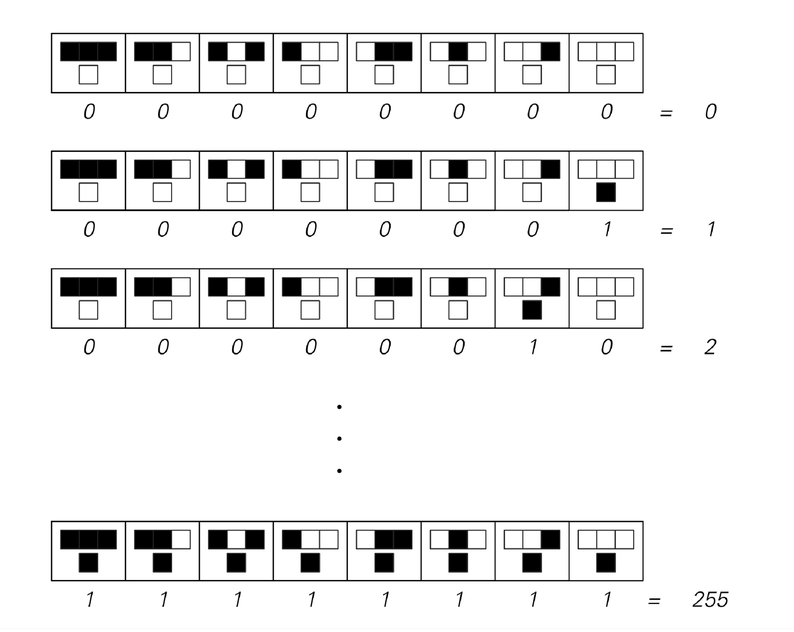
The sequence of 256 possible cellular automaton rules of the kind shown above. As indicated, the rules can conveniently be numbered from 0 to 255. The number assigned is such that when written in base 2, it gives a sequence of 0's and 1's that correspond to the sequence of new colors chosen for each of the eight possible cases covered by the rule.



