do not also show sensitive dependence on initial conditions. And indeed the pictures below illustrate that even in such cases changes in digit sequences are progressively amplified—just like in the shift map case (d).
But the crucial point that I will discuss more in Chapter 7 is that the presence of sensitive dependence on initial conditions in systems like (a) and (b) in no way implies that it is what is responsible for the randomness and complexity we see in these systems. And indeed, what looking at the shift map in terms of digit sequences shows us is that this phenomenon on its own can make no contribution at all to what we can reasonably consider the ultimate production of randomness.
Continuous Cellular Automata
Despite all their differences, the various kinds of programs discussed in the previous chapter have one thing in common: they are all based on elements that can take on only a discrete set of possible forms, typically just colors black and white. And in this chapter, we have introduced a similar kind of discreteness into our study of systems based on numbers
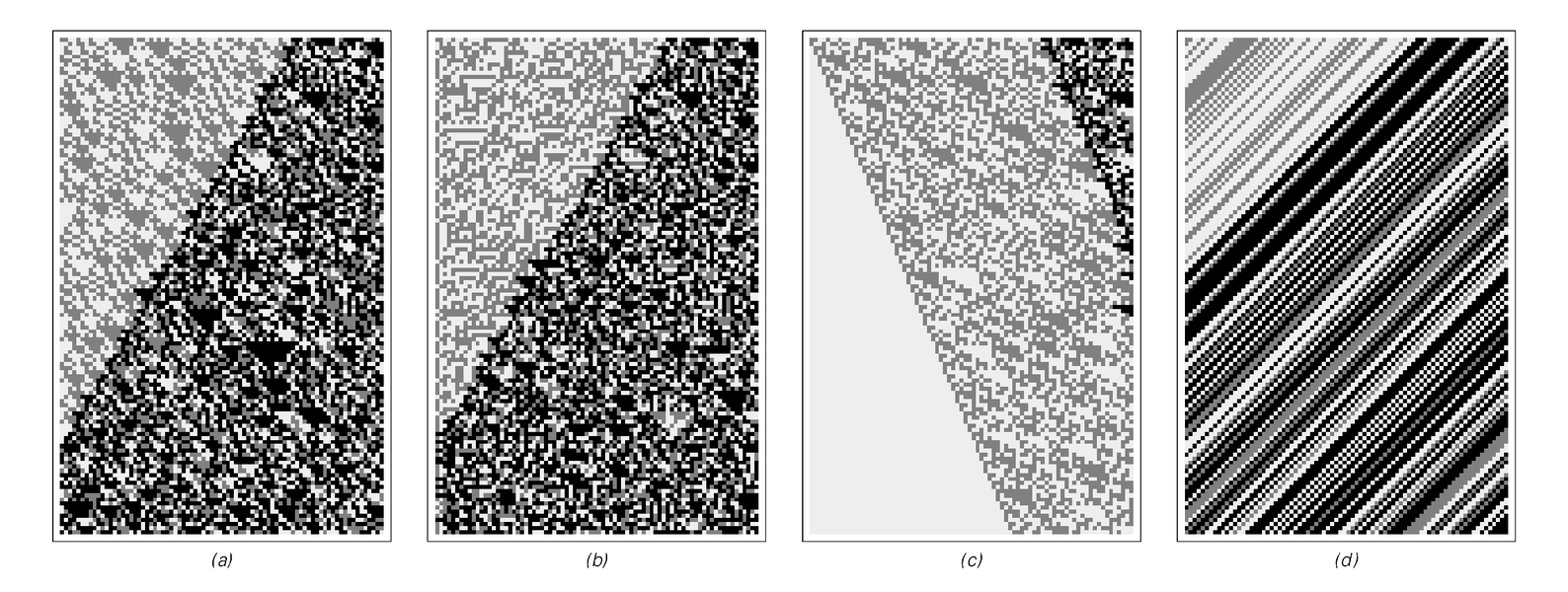
Differences in digit sequences produced by a small change in initial conditions for the four iterated maps discussed in this section. Cases (a), (b) and (d) exhibit sensitive dependence on initial conditions, in the sense that a change in insignificant digits far to the right eventually grows to affect all digits. Case (c) does not show such sensitivity to initial conditions, but instead always evolves to 0, independent of its initial conditions.



