fifty or so years, it has almost never been possible to demonstrate that results obtained from such approximations even correctly reproduce what the original mathematical equations would imply.
Models based on simple programs, however, suffer from no such problems. For essentially all of them involve only discrete elements which can be handled quite directly on a practical computer. And this means that it becomes straightforward in principle—and often highly efficient in practice—to work out at least the basic consequences of such models.
Many of the models that I discuss in this chapter are actually based on some of the very simplest kinds of programs that I consider anywhere in this book. But as we shall see, even these models appear quite sufficient to capture the behavior of a remarkably wide range of systems from nature and elsewhere—establishing beyond any doubt, I believe, the practical value of thinking in terms of simple programs.
The Growth of Crystals
At a microscopic level crystals consist of regular arrays of atoms laid out much like the cells in a cellular automaton. A crystal forms when a liquid or gas is cooled below its freezing point. Crystals always start from a seed—often a foreign object such as a grain of dust—and then grow by progressively adding more atoms to their surface.
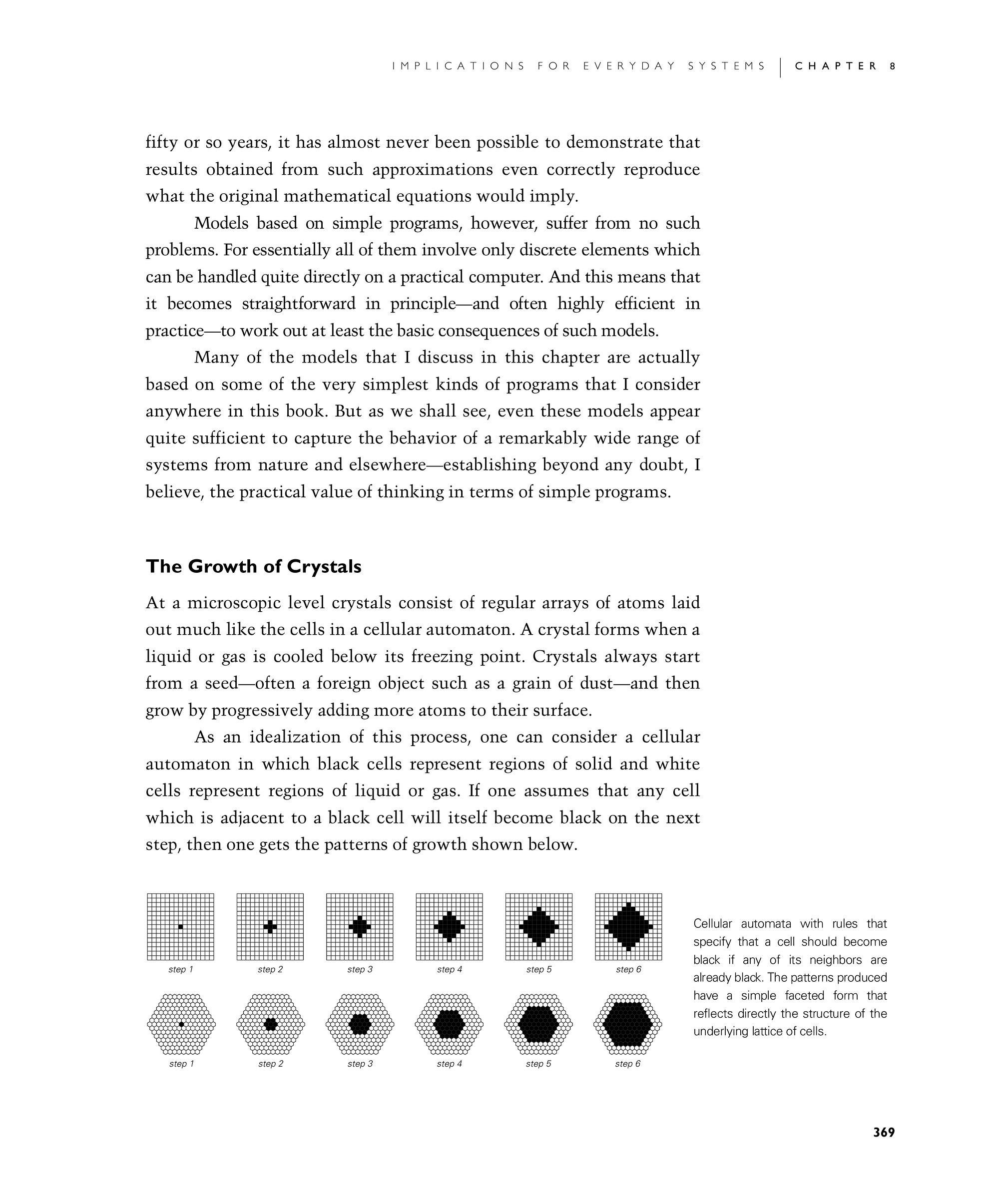
As an idealization of this process, one can consider a cellular automaton in which black cells represent regions of solid and white cells represent regions of liquid or gas. If one assumes that any cell which is adjacent to a black cell will itself become black on the next step, then one gets the patterns of growth shown below.


Cellular automata with rules that specify that a cell should become black if any of its neighbors are already black. The patterns produced have a simple faceted form that reflects directly the structure of the underlying lattice of cells.