A couple of sections ago we saw that all class 3 systems have the property that the detailed patterns they produce are highly sensitive to detailed changes in initial conditions. But despite this sensitivity at the level of details, the point is that any system like rule 22 or rule 30 yields patterns whose overall properties depend very little on the form of the initial conditions that are given.
By intrinsically generating randomness such systems in a sense have a certain fundamental stability: for whatever is done to their initial conditions, they still give the same overall random behavior, with the same large-scale properties. And as we shall see in the next few chapters, there are in fact many systems in nature whose apparent stability is ultimately a consequence of just this kind of phenomenon.
Special Initial Conditions
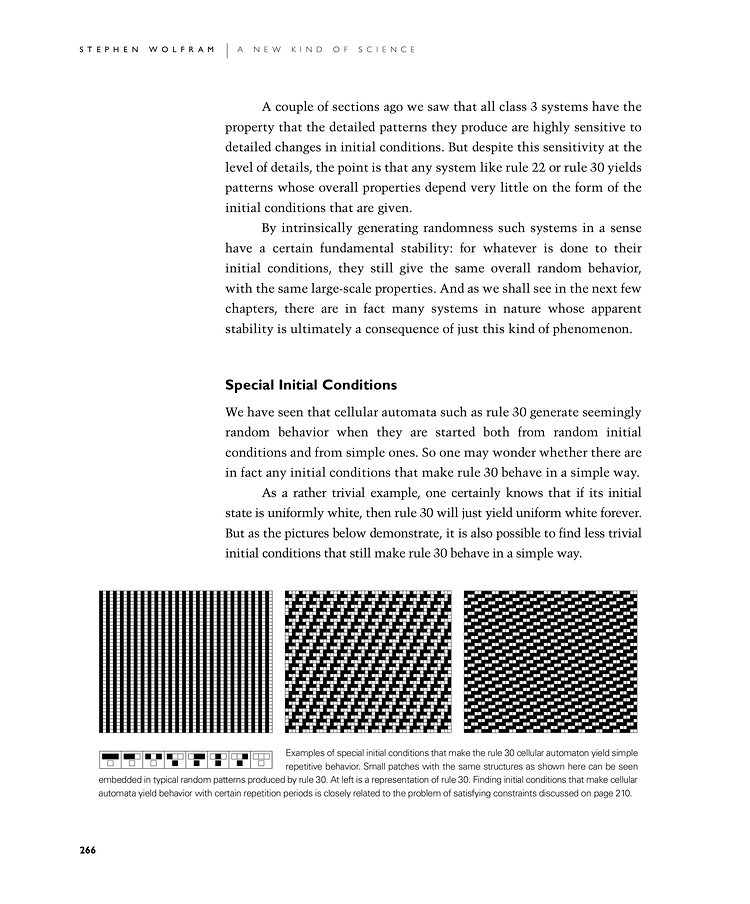
We have seen that cellular automata such as rule 30 generate seemingly random behavior when they are started both from random initial conditions and from simple ones. So one may wonder whether there are in fact any initial conditions that make rule 30 behave in a simple way.
As a rather trivial example, one certainly knows that if its initial state is uniformly white, then rule 30 will just yield uniform white forever. But as the pictures below demonstrate, it is also possible to find less trivial initial conditions that still make rule 30 behave in a simple way.

Examples of special initial conditions that make the rule 30 cellular automaton yield simple repetitive behavior. Small patches with the same structures as shown here can be seen embedded in typical random patterns produced by rule 30. At left is a representation of rule 30. Finding initial conditions that make cellular automata yield behavior with certain repetition periods is closely related to the problem of satisfying constraints discussed on page 210.