Practical details make it somewhat difficult to do systematic experiments on such programs. But the experiments I have carried out do suggest that, just as with simple register machines, searching through many millions of short programs typically yields at least a few that exhibit complex and seemingly random behavior.
Symbolic Systems
Register machines provide simple idealizations of typical low-level computer languages. But what about Mathematica? How can one set up a simple idealization of the transformations on symbolic expressions that Mathematica does? One approach suggested by the idea of combinators from the 1920s is to consider expressions with forms such as e[e[e][e]][e][e] and then to make transformations on these by repeatedly applying rules such as e[x_][y_]x[x[y]], where x_ and y_ stand for any expression.
The picture below shows an example of this. At each step the transformation is done by scanning once from left to right, and applying the rule wherever possible without overlapping.

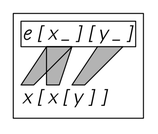
A sequence of steps in the evolution of a simple symbolic system. At each step each boxed region is transformed according to the rule shown. This transformation corresponds to applying the basic Mathematica operation expression /. rule.



