Multiway Systems
The network systems that we discussed in the previous section do not have any underlying grid of elements in space. But they still in a sense have a simple one-dimensional arrangement of states in time. And in fact, all the systems that we have considered so far in this book can be thought of as having the same simple structure in time. For all of them are ultimately set up just to evolve progressively from one state to the next.
Multiway systems, however, are defined so that they can have not just a single state, but a whole collection of possible states at any given step.
The picture below shows a very simple example of such a system.
Each state in the system consists of a sequence of elements, and in the particular case of the picture below, the rule specifies that at each step each of these elements either remains the same or is replaced by a pair of elements. Starting with a single state consisting of one element, the picture then shows that applying these rules immediately gives two possible states: one with a single element, and the other with two.
Multiway systems can in general use any sets of rules that define replacements for blocks of elements in sequences. We already saw exactly these kinds of rules when we discussed sequential substitution systems on page 88. But in sequential substitution systems the idea was to do just one replacement at each step. In multiway systems, however,
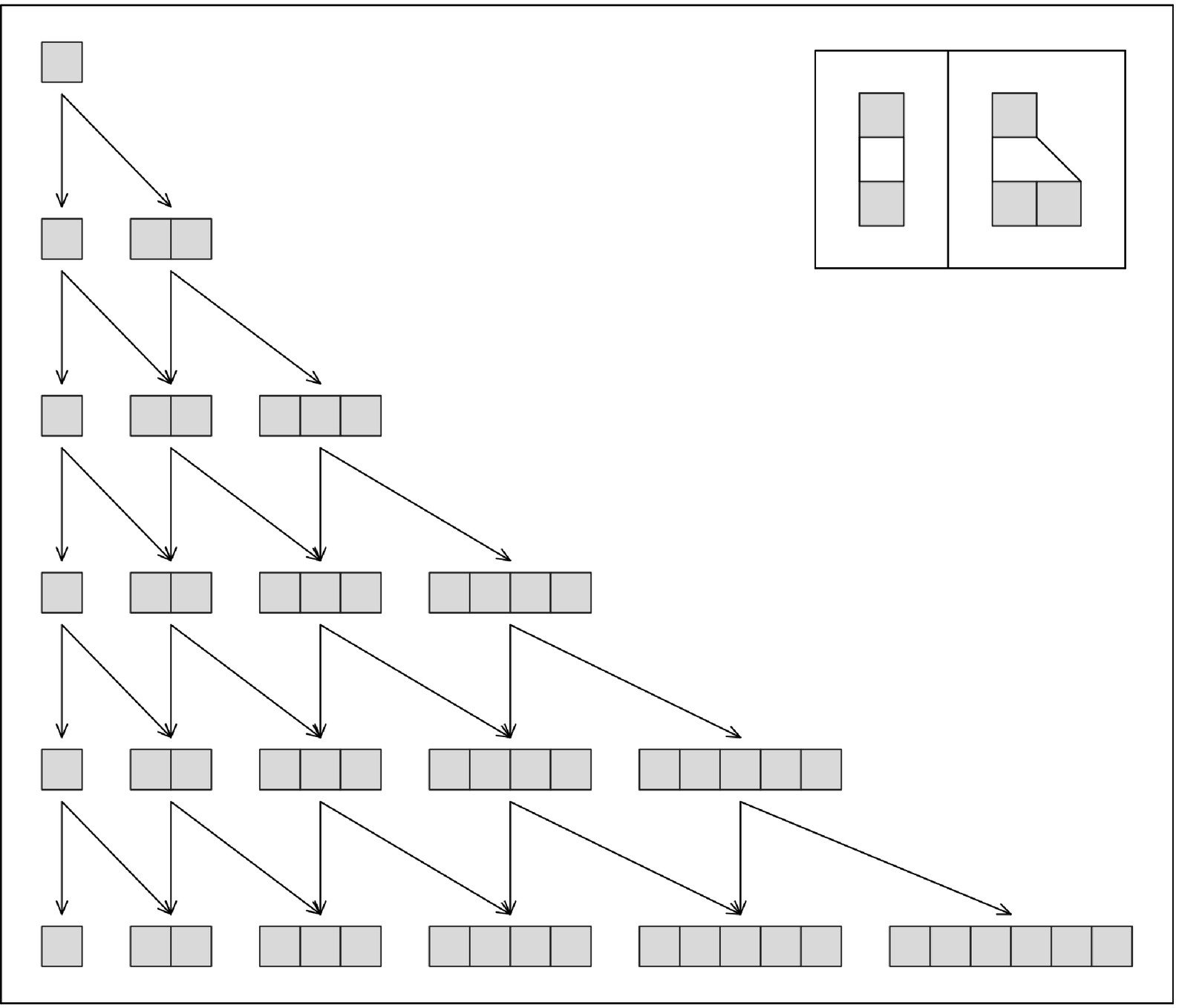
A very simple multiway system in which one element in each sequence is replaced at each step by either one or two elements. The main feature of multiway systems is that all the distinct sequences that result are kept.



