the idea is to do all possible replacements at each step—and then to keep all the possible different sequences that are generated.
The first set of pictures below show what happens with some very simple rules. In each of these examples the behavior turns out to be rather simple—with for example the number of possible sequences always increasing uniformly from one step to the next.
In general, however, this number need not exhibit such uniform growth, and the second set of pictures below show examples where fluctuations occur.
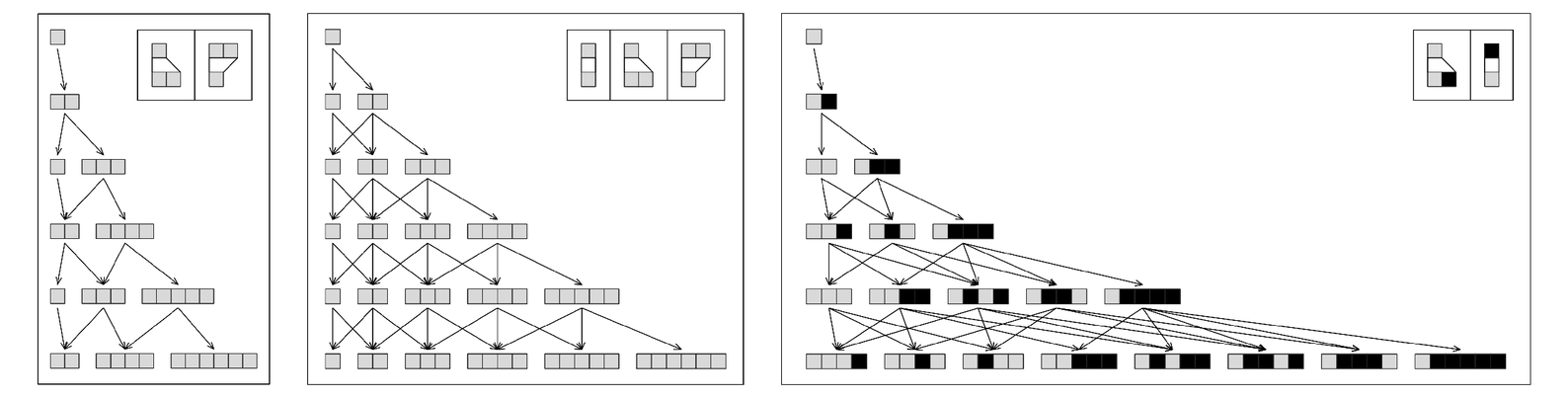
Examples of simple multiway systems. The number of distinct sequences at step t in these three systems is respectively Ceiling[t/2], t and Fibonacci[t+1] (which increases approximately like 1.618t).
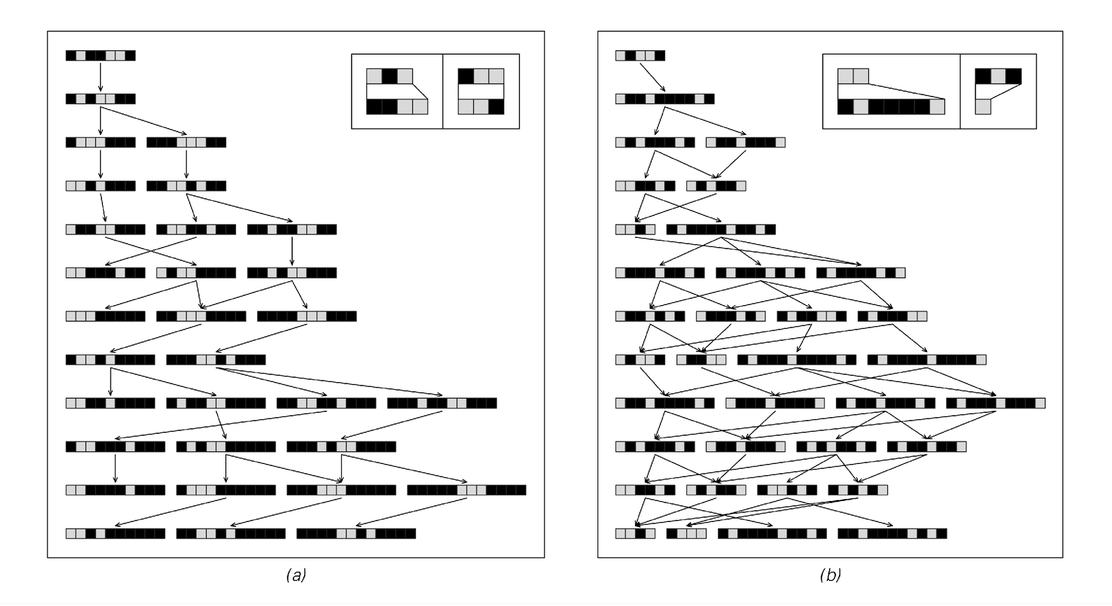 | 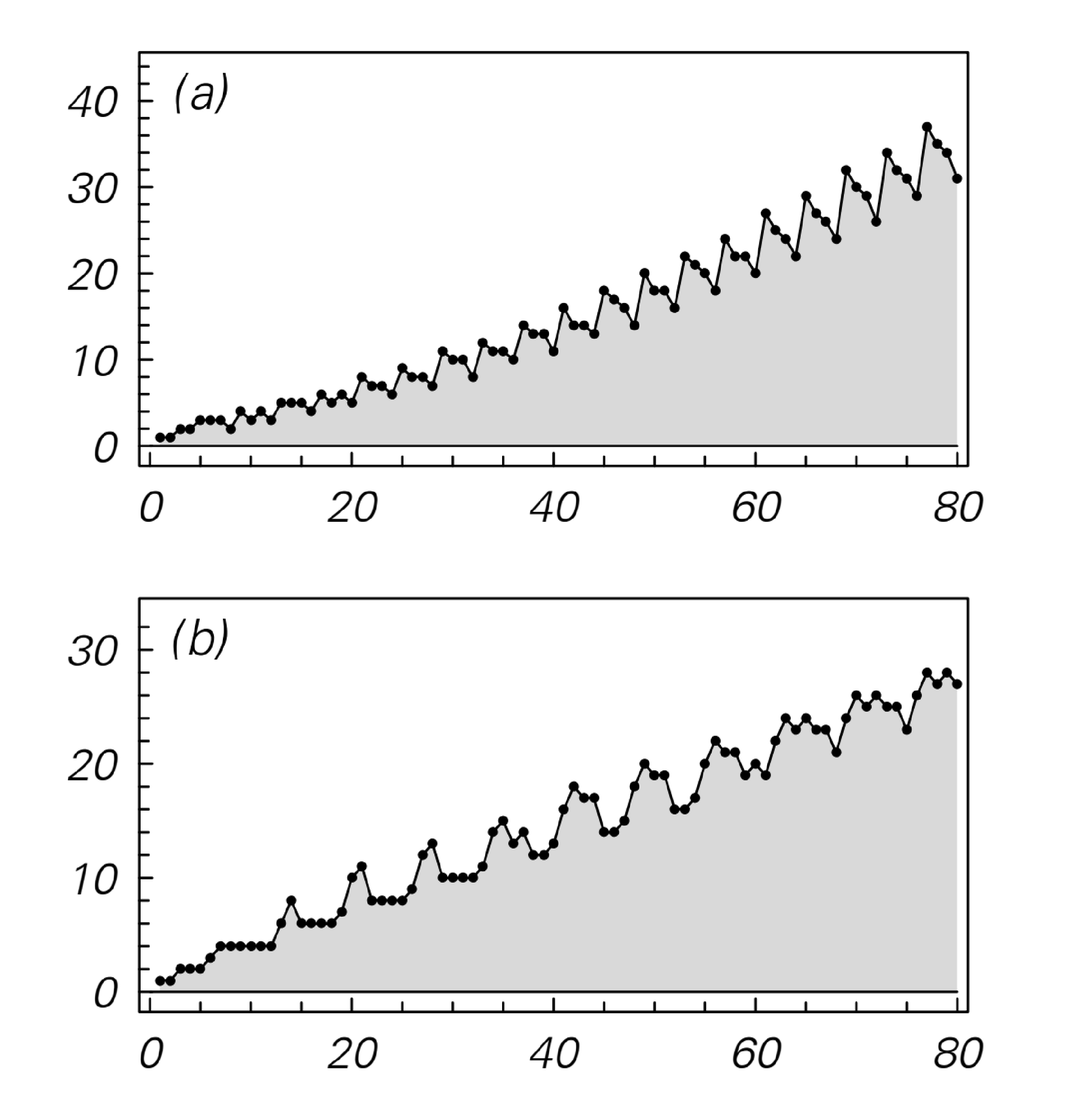 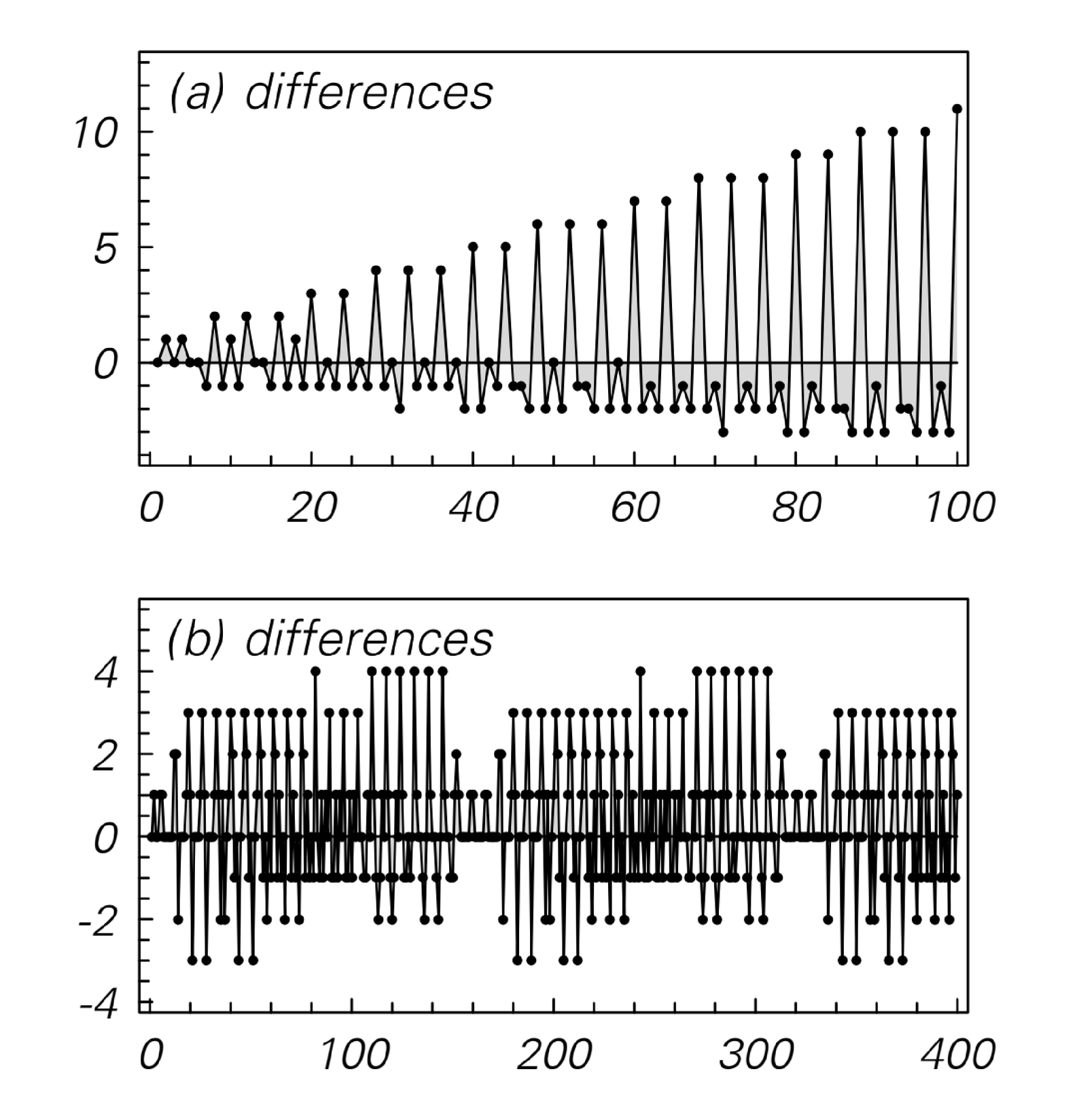 |
Examples of multiway systems with slightly more complicated behavior. The plots on the right show the total number of possible states obtained at each step, and the differences of these numbers from one step to the next. In both cases, essentially repetitive behavior is seen, every 40 and 161 steps respectively. Note that in case (a), the total number of possible states at step t increases roughly like t2, while in case (b) it increases only like t.



