Space, Time and Relativity
Several sections ago I argued that as observers within the universe everything we can observe must at some level be associated purely with the network of causal connections between events in the universe. And in the past few sections [10, 11, 12] I have outlined a series of types of models for how such a causal network might actually get built up.
But how do the properties of causal networks relate to our normal notions of space and time? There turn out to be some slight subtleties—but these seem to be exactly what end up yielding the theory of relativity.
As we saw in earlier sections [9, 10, 11], if one has an explicit evolution history for a system it is straightforward to deduce a causal network from it. But given only a causal network, what can one say about the evolution history?
The picture below shows an example of how successive steps in a particular evolution history can be recovered from a particular set of slices through the causal network derived from it. But what if one were to choose a different set of slices? In general, the sequence of strings that one would get would not correspond to anything that could arise from the same underlying substitution system.
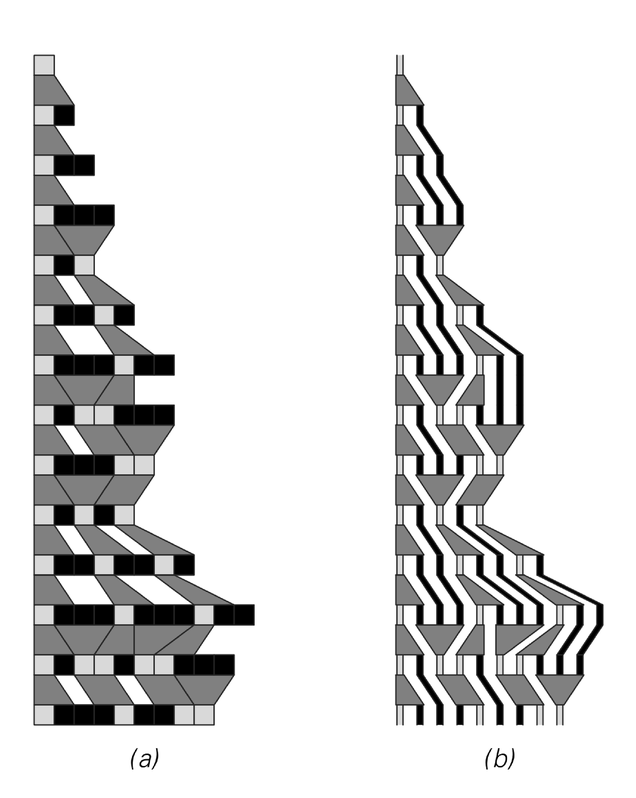  | 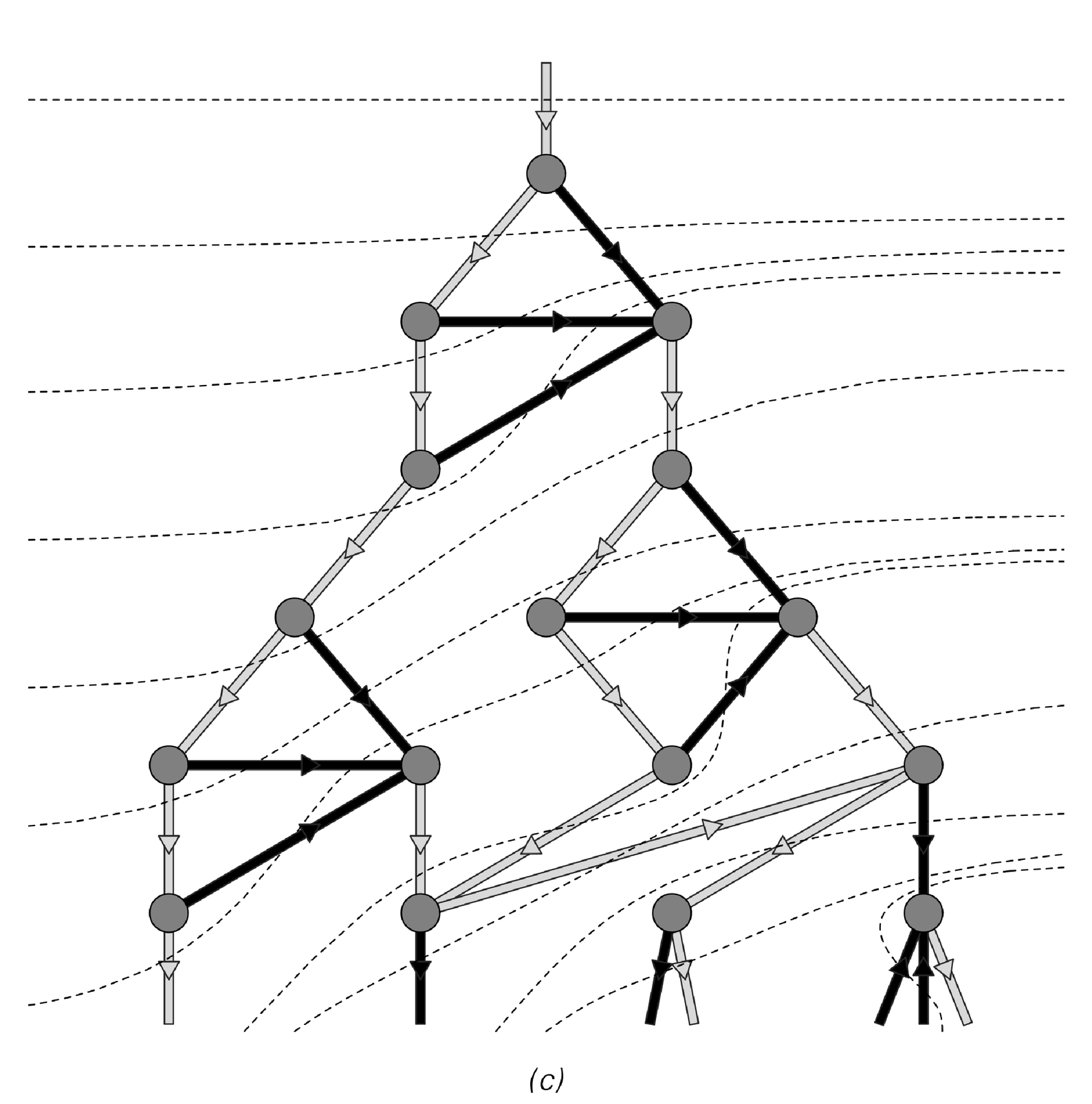 |
An example of how the succession of states in an evolution history can be recovered by taking appropriate slices through a causal network. Any consistent choice of such slices will correspond to a possible evolution history—with the same underlying rules, but potentially a different scheme for determining the order in which to apply replacements.



