But among slightly larger clusters there turn out to be many that do not overlap themselves—and indeed this becomes common as soon as there are at least two connections between each dangling one.
The first few examples are shown below. And in almost all of these, there is no overlap not only within a single cluster, but also between different clusters. And this means that rules based on replacements for collections of these clusters will have the property that the causal networks they produce are independent of the updating scheme used.
One feature of the various rules I showed earlier is that they all maintain planarity of networks—so that if one starts with a network that can be laid out in the plane without any lines crossing, then every subsequent network one gets will also have this property.
Yet in our everyday experience space certainly does not seem to have this property. But beyond the practical problem of displaying what happens, there is actually no fundamental difficulty in setting up rules that can generate non-planarity—and indeed many rules based on the clusters below will for example do this.
So in the end, if one manages to find the ultimate rules for the universe, my expectation is that they will give rise to networks that on a small scale look largely random. But this very randomness will most likely be what for example allows a definite and robust value of 3 to emerge for the dimensionality of space—even though all of the many complicated phenomena in our universe must also somehow be represented within the structure of the same network.
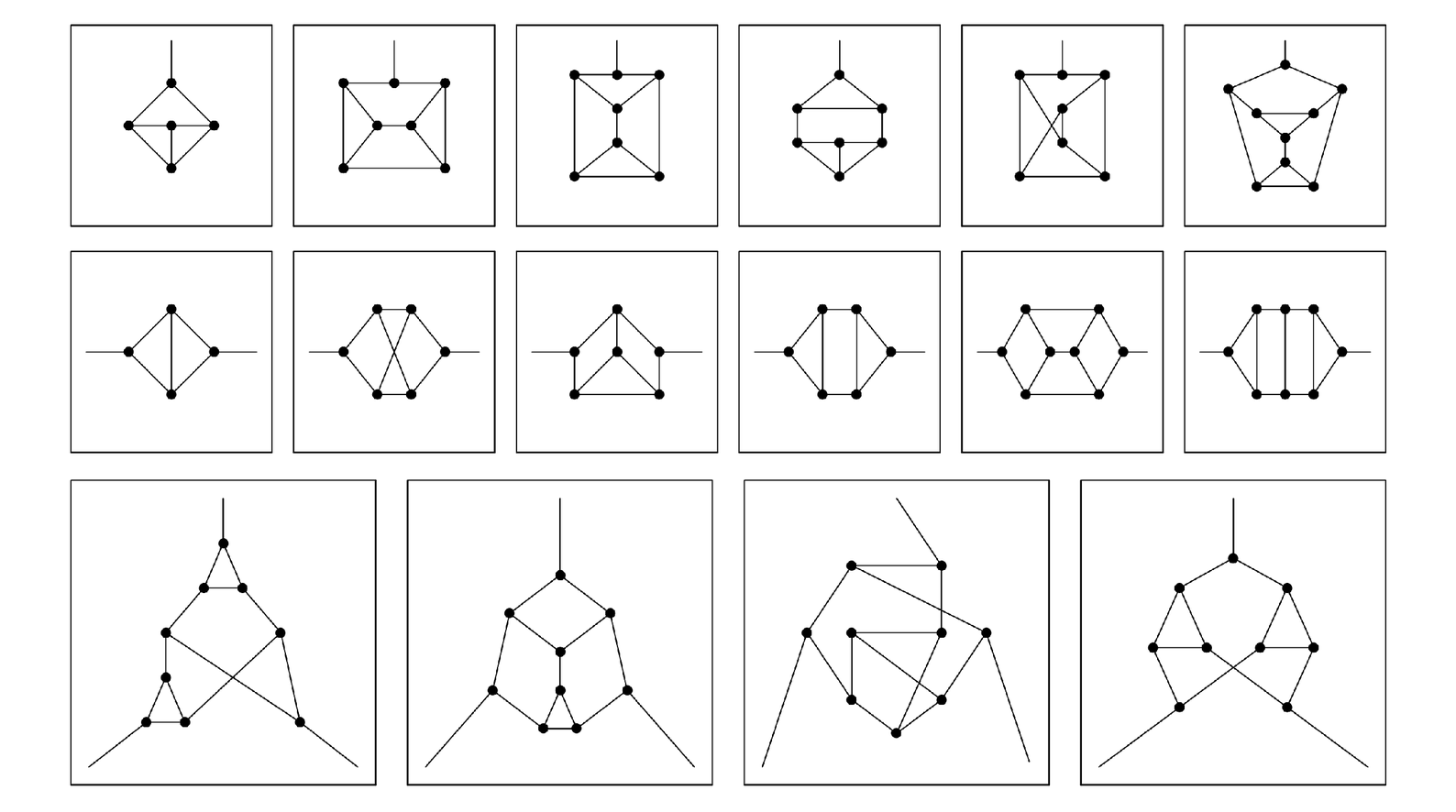
The simplest clusters that have no overlaps with themselves—and mostly have no overlaps with each other. Replacements for sets of clusters that do not overlap have the property of causal invariance.



