Just as for substitution systems on strings, one can find causal networks that represent the causal connections between different updating events on networks. And as an example the first set of pictures below show such causal networks for the evolution processes on the previous page.
In the rather simple case of rule (a) the results turn out to be independent of the updating scheme that was used. But for rules (b) and (c), different schemes in general yield different causal networks.
So what kinds of underlying replacement rules lead to causal networks that are independent of how the rules are applied? The situation is much the same as for strings—with the basic criterion just being that all replacements that appear in the rules should be for clusters of nodes that can never overlap themselves or each other.
The second set of pictures below show all possible distinct clusters with up to five nodes—and all but three of these already can overlap themselves.
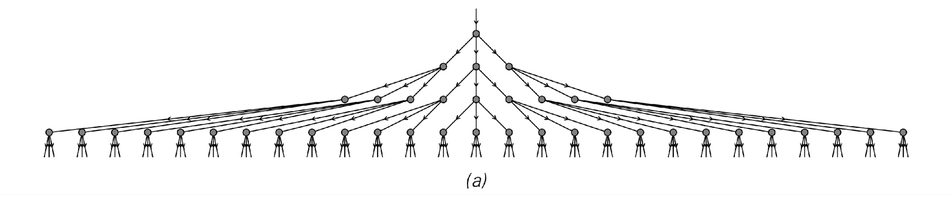 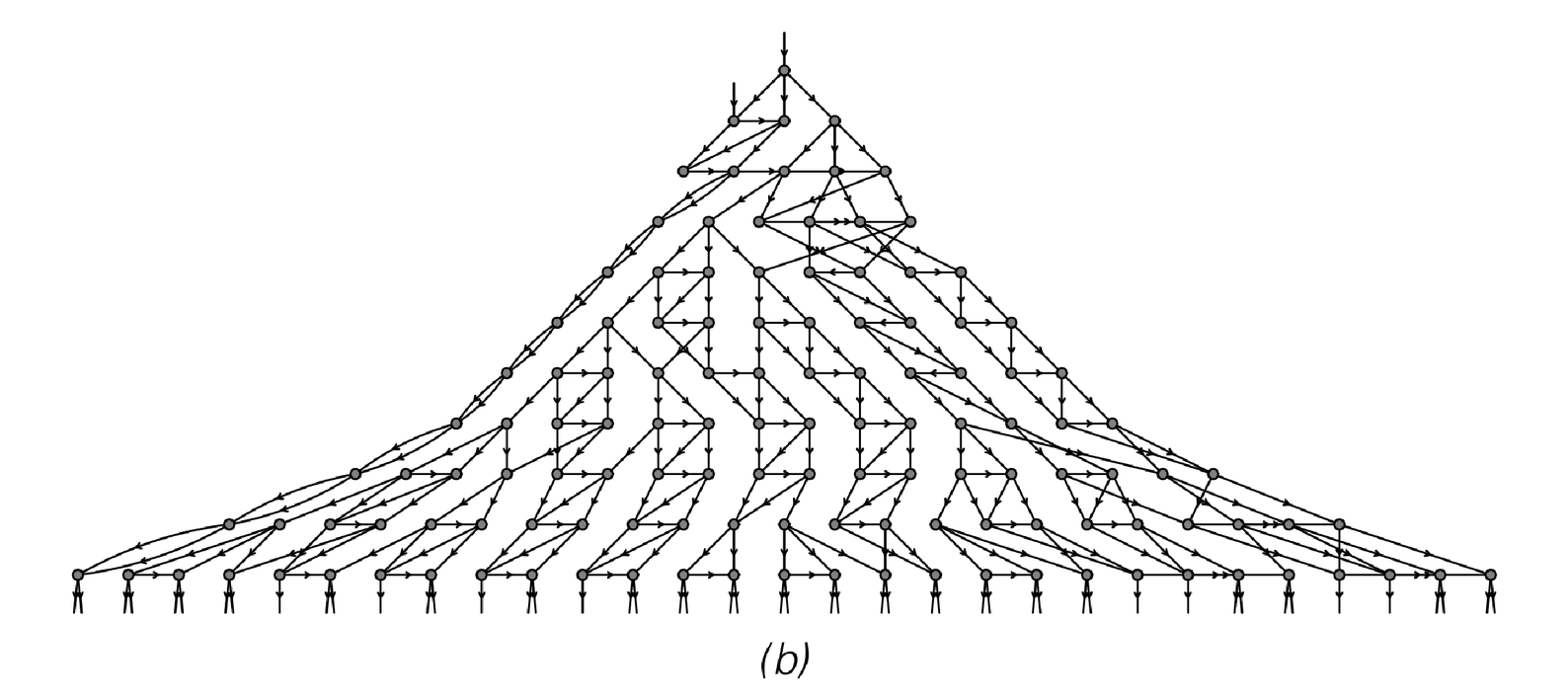 | 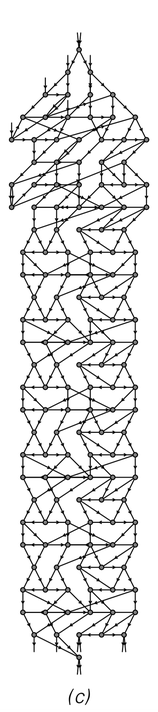 |
Causal networks that represent the relationship between updating events for the network evolution processes shown on the previous page.

All possible distinct clusters containing up to five nodes, with planarity not required.



