The Notion of Attractors
In this chapter we have seen many examples of patterns that can be produced by starting from random initial conditions and then following the evolution of cellular automata for many steps.
But what can be said about the individual configurations of black and white cells that appear at each step? In random initial conditions, absolutely any sequence of black and white cells can be present. But it is a feature of most cellular automata that on subsequent steps the sequences that can be produced become progressively more restricted.
The first picture below shows an extreme example of a class 1 cellular automaton in which after just one step the only sequences that can occur are those that contain only black cells.
The resulting configuration can be thought of as a so-called attractor for the cellular automaton evolution. It does not matter what initial conditions one starts from: one always reaches the same all-black attractor in the end. The situation is somewhat similar to what happens in a mechanical system like a physical pendulum. One can start the pendulum swinging in any configuration, but it will always tend to evolve to the configuration in which it is hanging straight down.
The second picture below shows a class 2 cellular automaton that once again evolves to an attractor after just one step. But now the attractor does not just consist of a single configuration, but instead
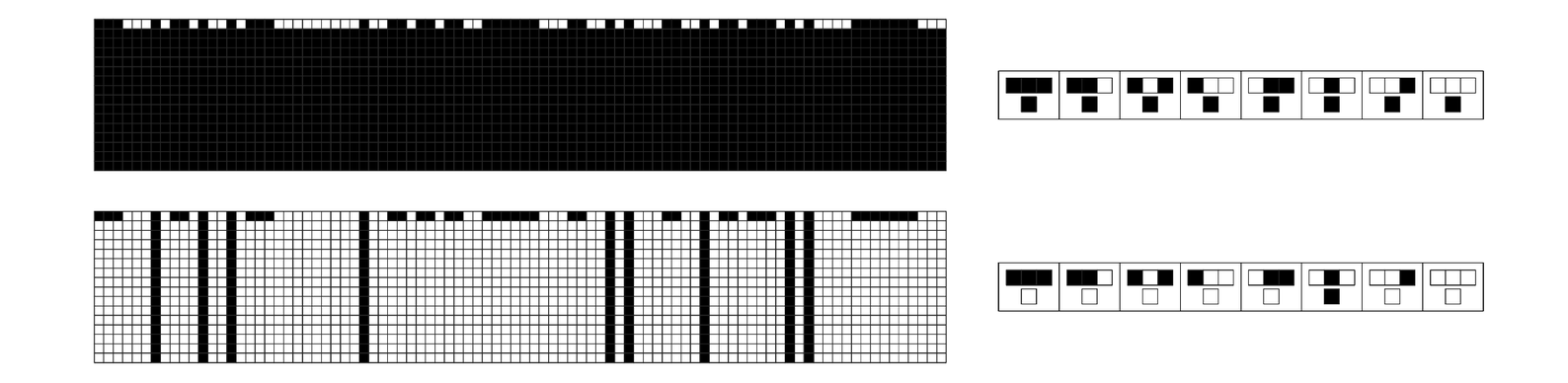
Examples of simple cellular automata that evolve after just one step to attractors in which only certain sequences of black and white cells can occur. In the first case, the sequences that can occur are ones that involve only black cells. In the second case, the sequences are ones in which every black cell is surrounded by white cells. The rules shown are numbers 255 and 4.



