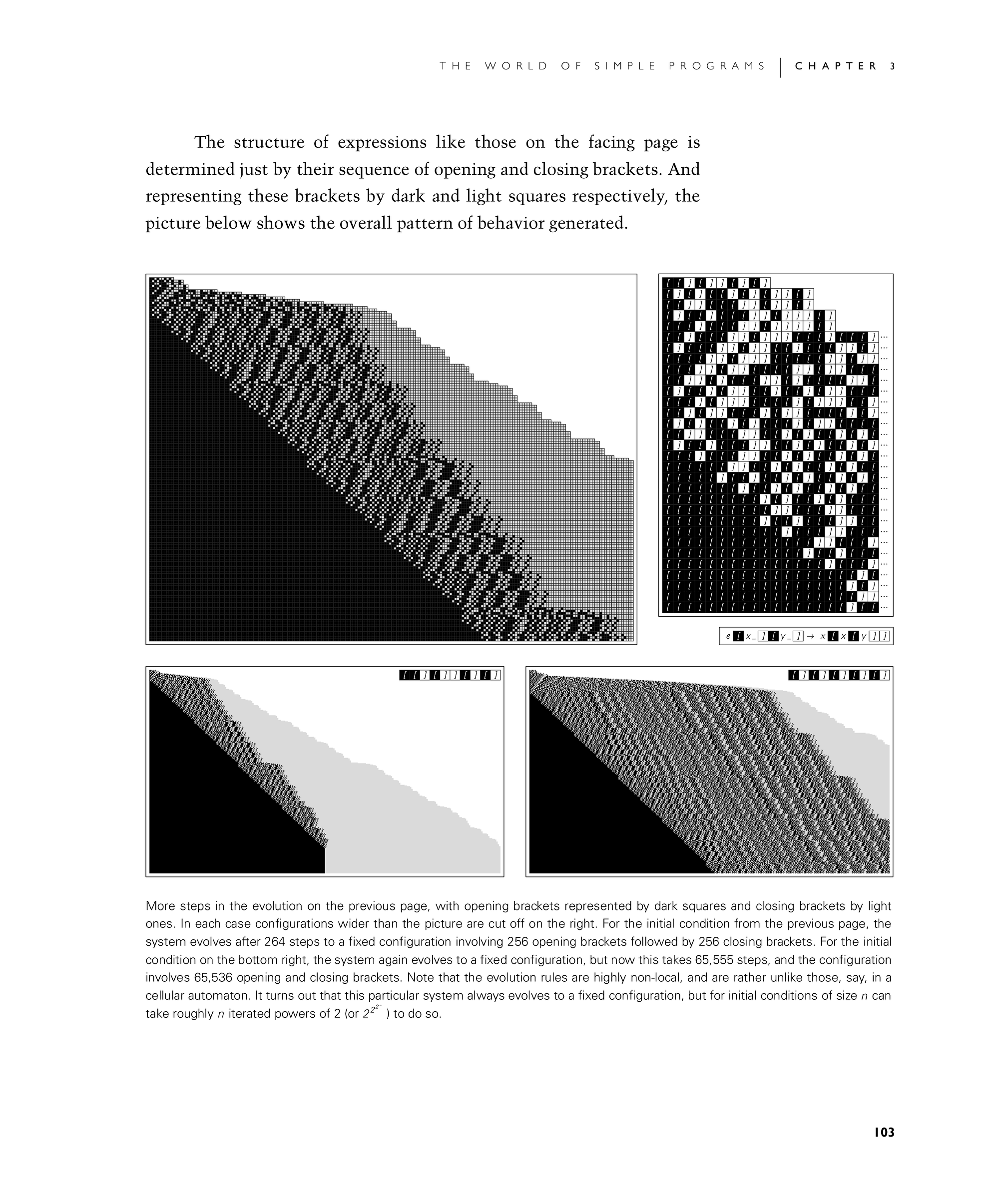
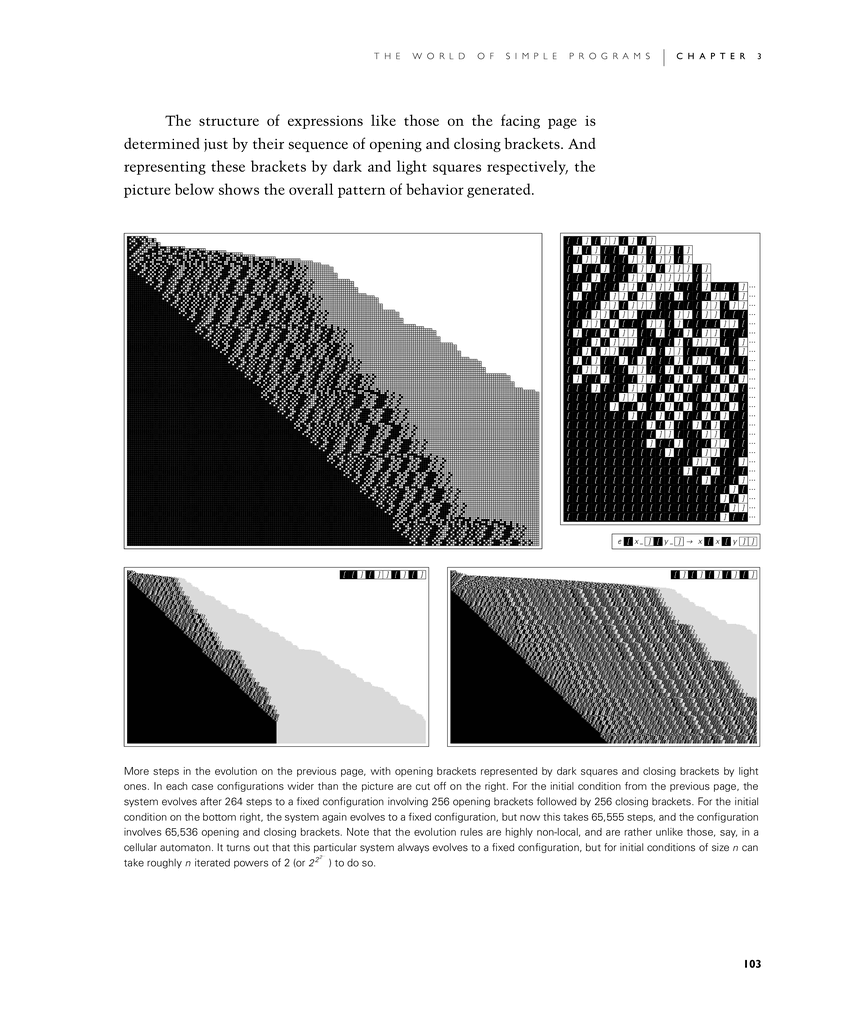
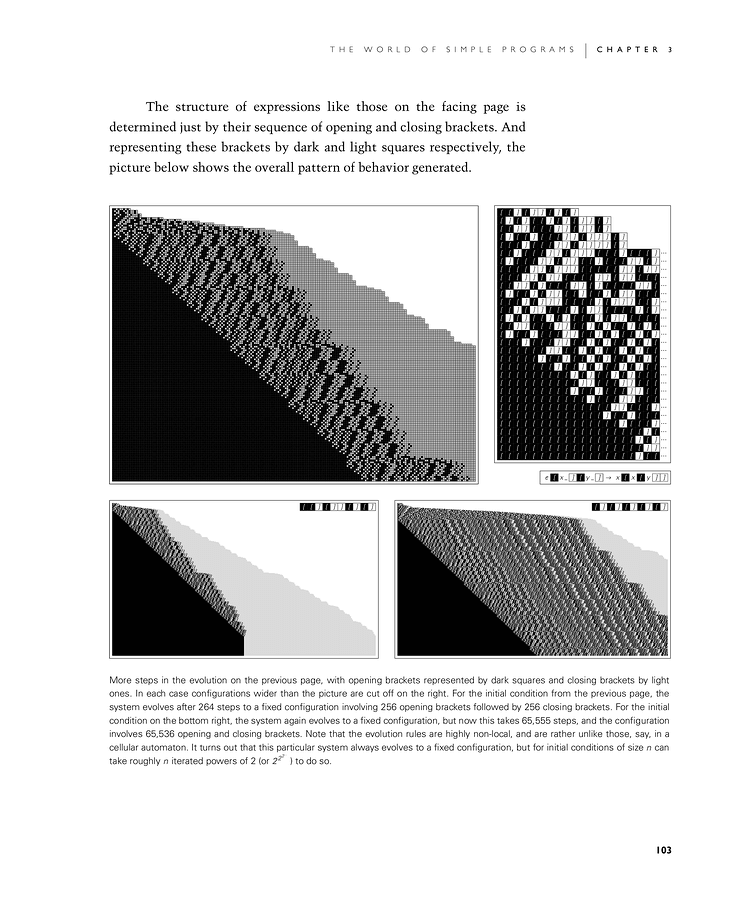
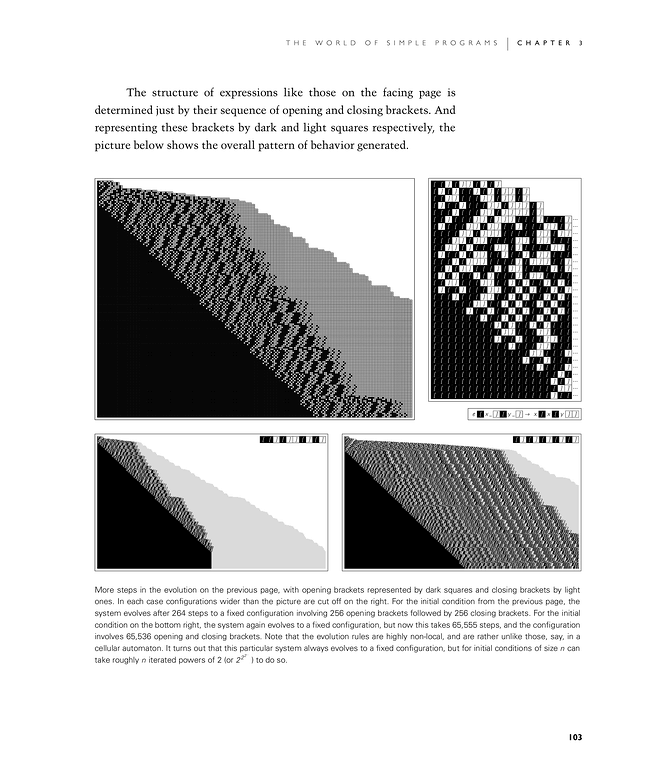
The structure of expressions like those on the facing page is determined just by their sequence of opening and closing brackets. And representing these brackets by dark and light squares respectively, the picture below shows the overall pattern of behavior generated.
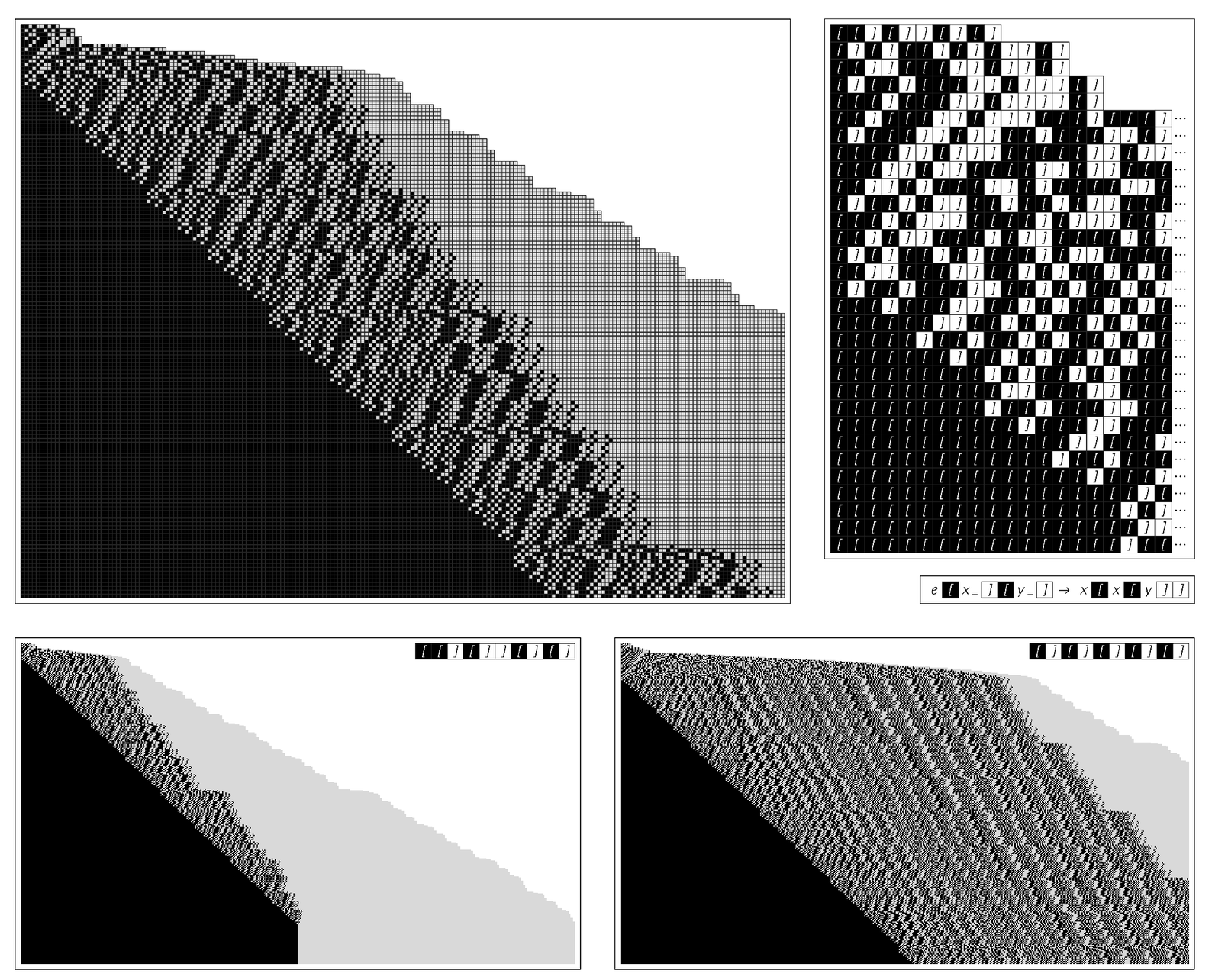
More steps in the evolution on the previous page, with opening brackets represented by dark squares and closing brackets by light ones. In each case configurations wider than the picture are cut off on the right. For the initial condition from the previous page, the system evolves after 264 steps to a fixed configuration involving 256 opening brackets followed by 256 closing brackets. For the initial condition on the bottom right, the system again evolves to a fixed configuration, but now this takes 65,555 steps, and the configuration involves 65,536 opening and closing brackets. Note that the evolution rules are highly non-local, and are rather unlike those, say, in a cellular automaton. It turns out that this particular system always evolves to a fixed configuration, but for initial conditions of size n can take roughly n iterated powers of 2 (or 222…) to do so.