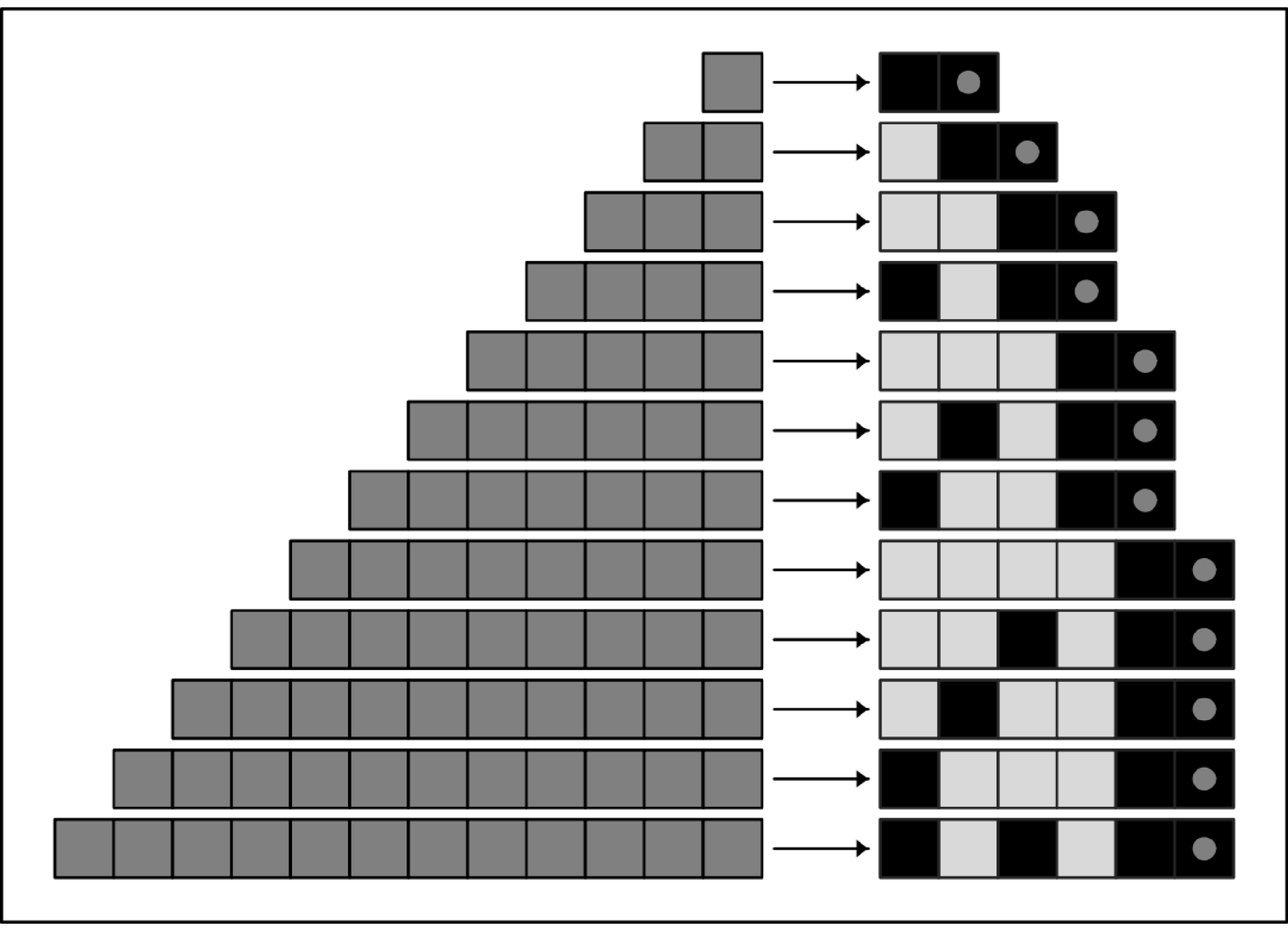
Indeed, any digit sequence can be thought of as providing a short representation for a number. But for run-length encoding it turns out that ordinary base 2 digit sequences do not quite work. For if the numbers corresponding to the lengths of successive runs are given one after another then there is no way to tell where the digits of one number end and the next begin.

Several approaches can be used, however, to avoid this problem. One, illustrated in picture (c) at the bottom of the facing page, is to insert at the beginning of each number a specification of how many digits the number contains. Another approach, illustrated in picture (d), is in effect to have two cells representing each digit, and then to indicate the end of the number by a pair of black cells. A variant on this approach, illustrated in picture (e), uses a non-integer base in which pairs of black cells can occur only at the end of a number.

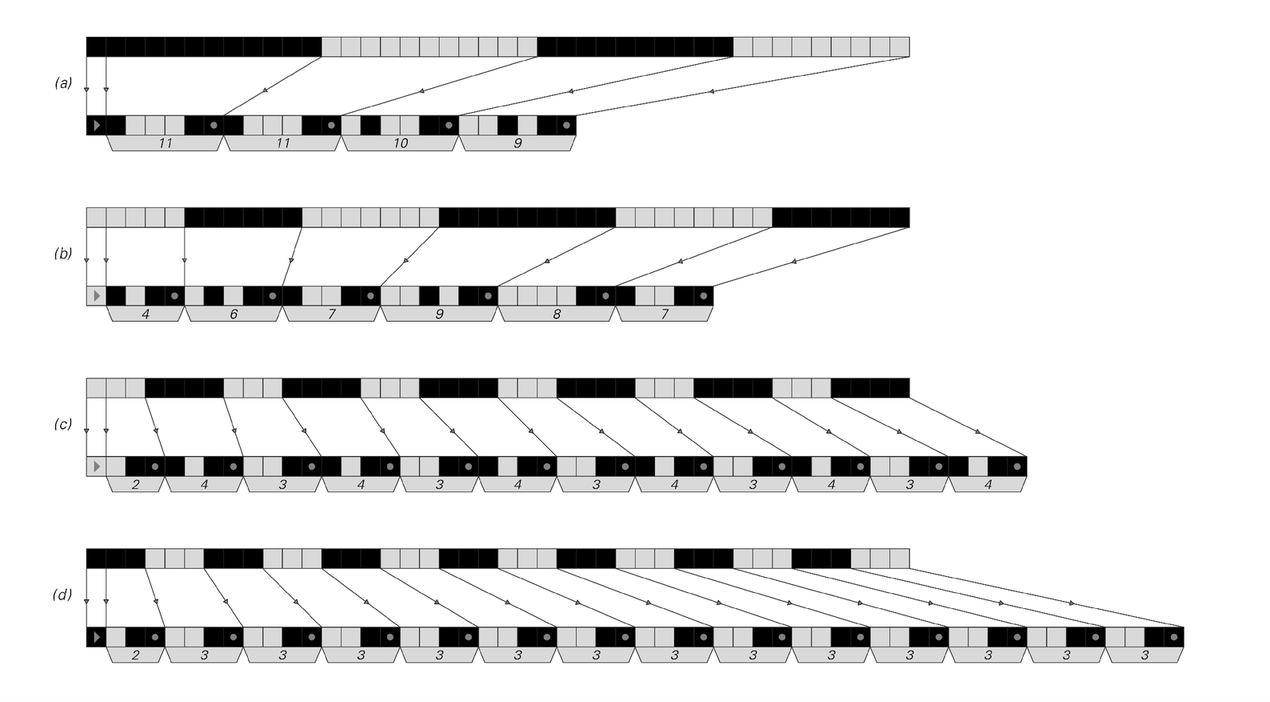Examples of run-length encoding. In each case the input data is shown on top, and the output is shown below. The arrows between input and output show how the data is broken into runs of identical elements. Each run is then specified by a number, represented as a sequence ending with two black cells, as indicated in the inset picture, and in picture (e) on the facing page. For the first two sets of input data there are enough long runs present that compression is achieved. But for the other two sets no compression is achieved. Note that the first cell in the output is used to specify whether the first run is black or white. In this picture and those that follow, the output consists purely of black and white cells; the gray annotations are included purely as aids to interpretation.