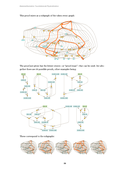
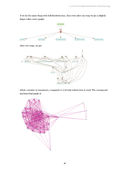
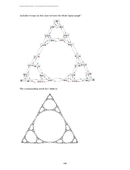
Abstract
Both metamathematics and physics are posited to emerge from samplings by observers of the unique ruliad structure that corresponds to the entangled limit of all possible computations. The possibility of higher-level mathematics accessible to humans is posited to be the analog for mathematical observers of the perception of physical space for physical observers. A physicalized analysis is given of the bulk limit of traditional axiomatic approaches to the foundations of mathematics, together with explicit empirical metamathematics of some examples of formalized mathematics. General physicalized laws of mathematics are discussed, associated with concepts such as metamathematical motion, inevitable dualities, proof topology and metamathematical singularities. It is argued that mathematics as currently practiced can be viewed as derived from the ruliad in a direct Platonic fashion analogous to our experience of the physical world, and that axiomatic formulation, while often convenient, does not capture the ultimate character of mathematics. Among the implications of this view is that only certain collections of axioms may be consistent with inevitable features of human mathematical observers. A discussion is included of historical and philosophical connections, as well as of foundational implications for the future of mathematics.