As we’ve just seen, the accumulative evolution of even very simple transformation rules for expressions can quickly lead to considerable complexity. And in an effort to understand the essence of what’s going on, it’s useful to look at the slightly simpler case not of rules for “tree-structured expressions” but instead at rules for strings of characters.
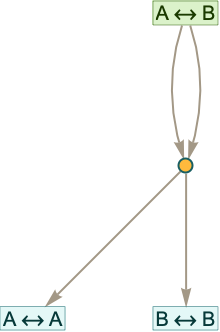
Consider the seemingly trivial case of the rule:
After one step this gives
while after 2 steps we get
though treating uv as the same as vu this just becomes:
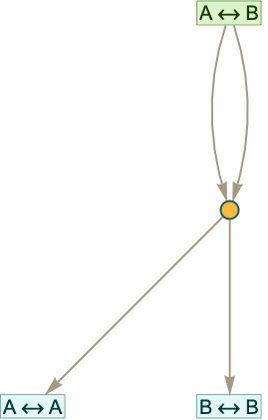
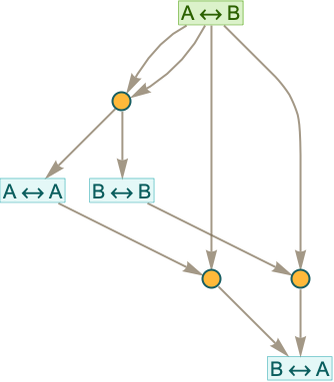
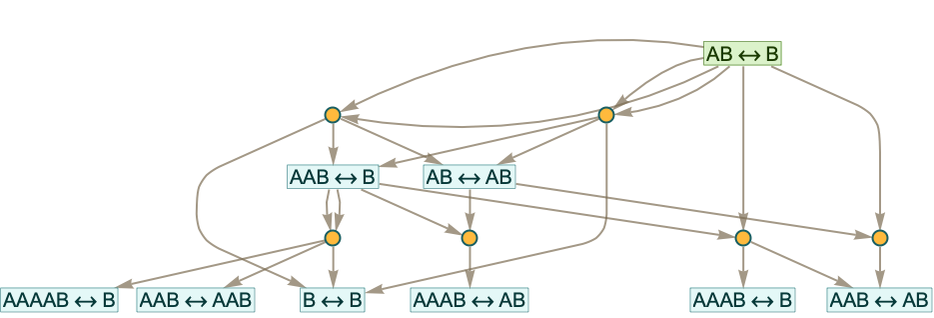
Here’s what happens with the rule:
After 2 steps we get
and after 3 steps
where now there are a total of 25 “theorems”, including (unsurprisingly) things like:
It’s worth noting that despite the “lexical similarity” of the string rule ABB we’re now using to the expression rule a∘bb from the previous section, these rules actually work in very different ways. The string rule can apply to characters anywhere within a string, but what it inserts is always of fixed size. The expression rule deals with trees, and only applies to “whole subtrees”, but what it inserts can be a tree of any size. (One can align these setups by thinking of strings as expressions in which characters are “bound together” by an associative operator, as in A·B·A·A. But if one explicitly gives associativity axioms these will lead to additional pieces in the token-event graph.)
A rule like a_∘b_b_ also has the feature of involving patterns. In principle we could include patterns in strings too—both for single characters (as with _) and for sequences of characters (as with __)—but we won’t do this here. (We can also consider one-way rules, using instead of .)
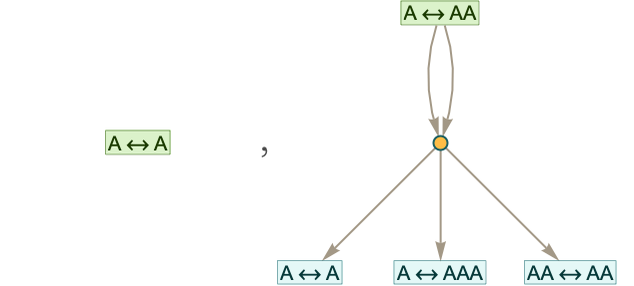
To get a general sense of the kinds of things that happen in accumulative (string) systems, we can consider enumerating all possible distinct two-way string transformation rules. With only a single character A, there are only two distinct cases
because AAA systematically generates all possible An Am rules
and at t steps gives a total number of rules equal to:
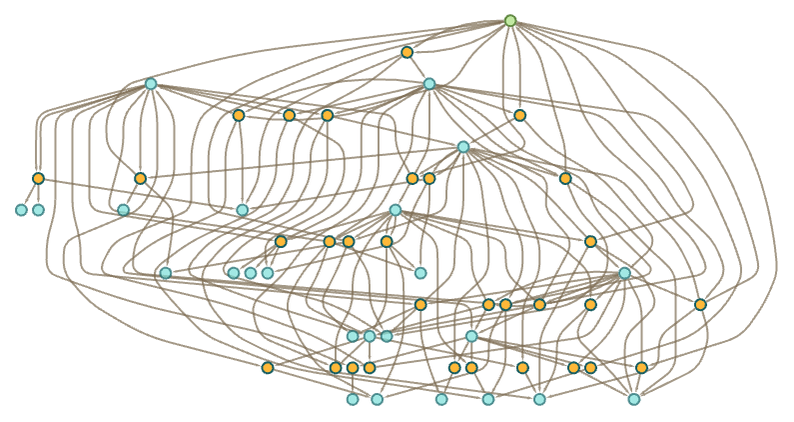
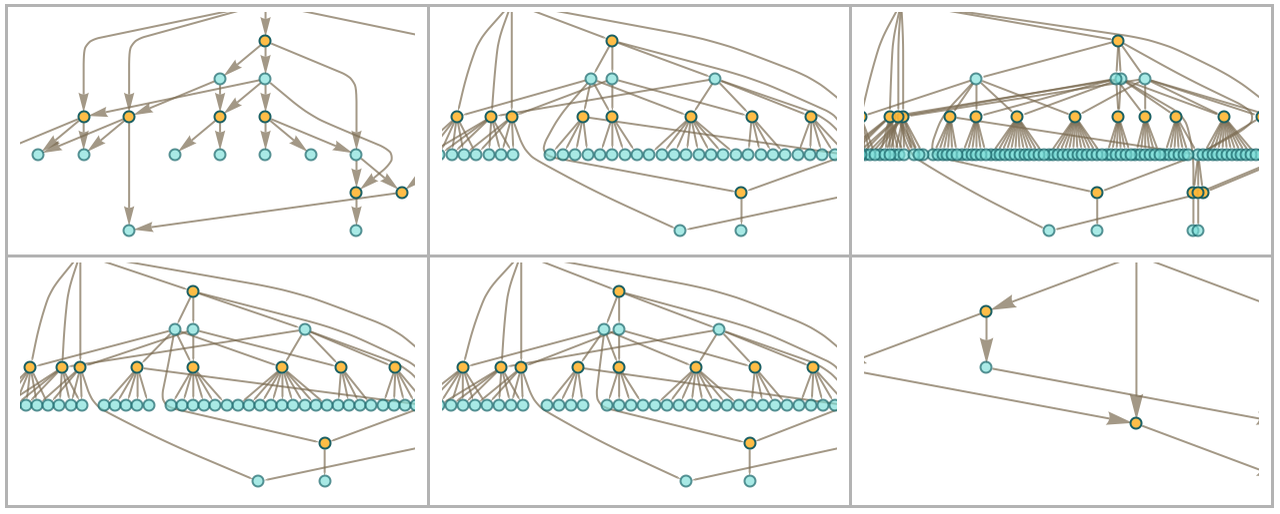
With characters A and B the distinct token-event graphs generated starting from rules with a total of at most 5 characters are:
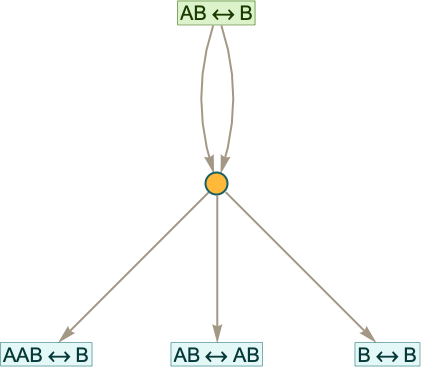
Note that when the strings in the initial rule are the same length, only a rather trivial finite token-event graph is ever generated, as in the case of AAAB:
But when the strings are of different lengths, there is always unbounded growth.