We’ve talked about what happens with specific, sample axiom systems, as well as with various axiom systems that have arisen in present-day mathematics. But what about “axiom systems in the wild”—say just obtained by random sampling, or by systematic enumeration? In effect, each possible axiom system can be thought of as “defining a possible field of mathematics”—just in most cases not one that’s actually been studied in the history of human mathematics. But the ruliad certainly contains all such axiom systems. And in the style of A New Kind of Science we can do ruliology to explore them.
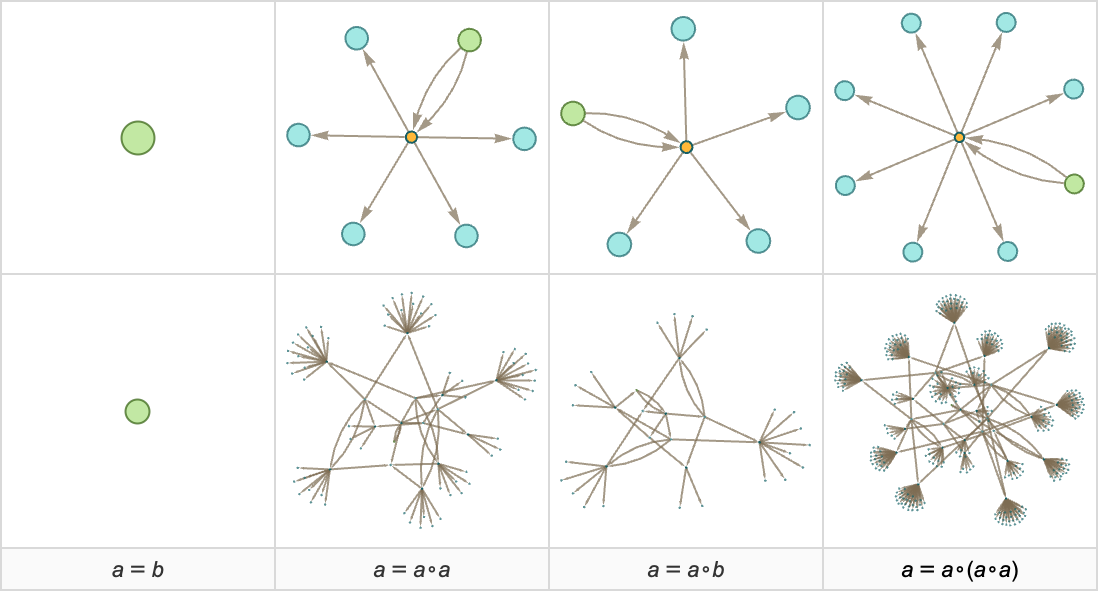
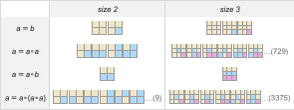
As an example, let’s look at axiom systems with just one axiom, one binary operator and one or two variables. Here are the smallest few:
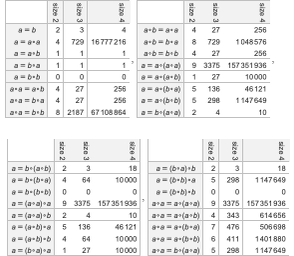
For each of these axiom systems, we can then ask what theorems they imply. And for example we can enumerate theorems—just as we have enumerated axiom systems—then use automated theorem proving to determine which theorems are implied by which axiom systems. This shows the result, with possible axiom systems going down the page, possible theorems going across, and a particular square being filled in (darker for longer proofs) if a given theorem can be proved from a given axiom system:
The diagonal on the left is axioms “proving themselves”. The lines across are for axiom systems like a=b that basically say that any two expressions are equal—so that any theorem that is stated can be proved from the axiom system.
But what if we look at the whole entailment cone for each of these axiom systems? Here are a few examples of the first two steps:
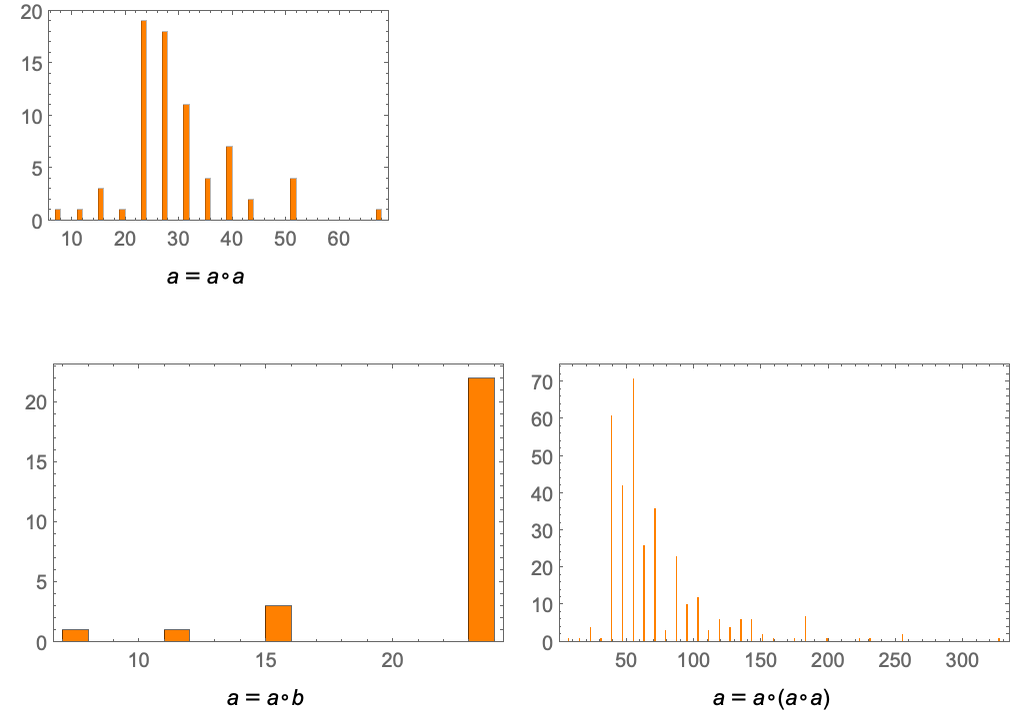
With our method of accumulative evolution the axiom a=b doesn’t on its own generate a growing entailment cone (though if combined with any axiom containing ∘ it does, and so does a=b∘c on its own). But in all the other cases shown the entailment cone grows rapidly (typically at least exponentially)—in effect quickly establishing many theorems. Most of those theorems, however, are “not small”—and for example after 2 steps here are the distributions of their sizes:
So let’s say we generate only one step in the entailment cone. This is the pattern of “small theorems” we establish:
And here is the corresponding result after two steps:
Superimposing this on our original array of theorems we get:
In other words, there are many small theorems that we can establish “if we look for them”, but which won’t “naturally be generated” quickly in the entailment cone (though eventually it’s inevitable that they will be generated). (Later we’ll see how this relates to the concept of “entailment fabrics” and the “knitting together of pieces of mathematics”.)
In the previous section we discussed the concept of models for axiom systems. So what models do typical “axiom systems from the wild” have? The number of possible models of a given size varies greatly for different axiom systems:
But for each model we can ask what theorems it implies are valid. And for example combining all models of size 2 yields the following “predictions” for what theorems are valid (with the actual theorems indicated by dots):
Using instead models of size 3 gives “more accurate predictions”:
As expected, looking at a fixed number of steps in the entailment cone “underestimates” the number of valid theorems, while looking at finite models overestimates it.
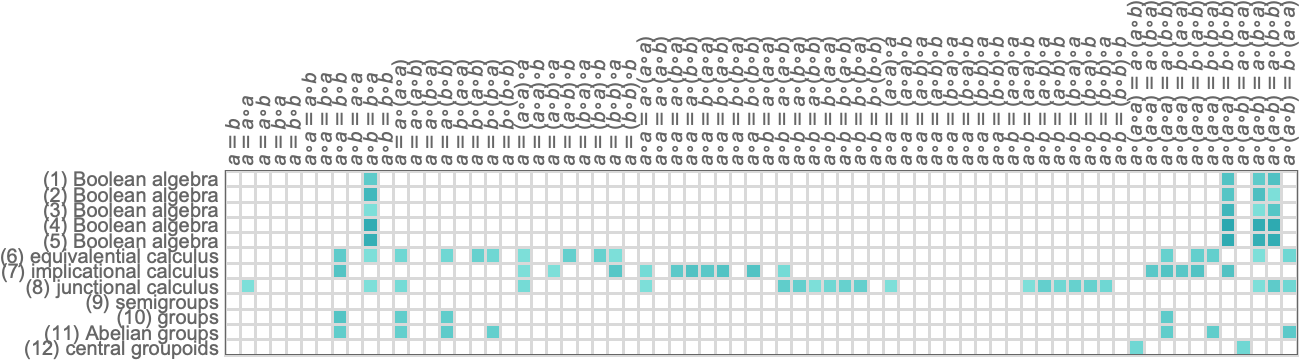
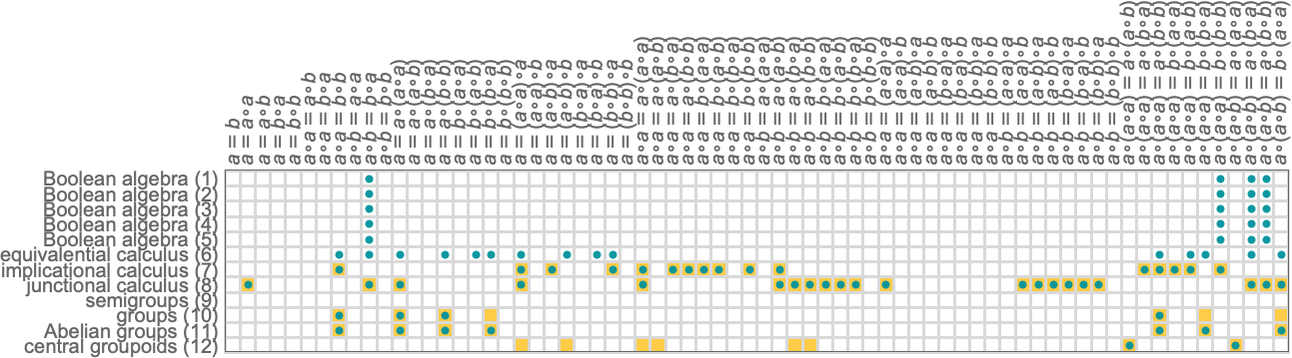
So how does our analysis for “axiom systems from the wild” compare with what we’d get if we considered axiom systems that have been explicitly studied in traditional human mathematics? Here are some examples of “known” axiom systems that involve just a single binary operator
and here’s the distribution of theorems they give:
As must be the case, all the axiom systems for Boolean algebra yield the same theorems. But axiom systems for “different mathematical theories” yield different collections of theorems.
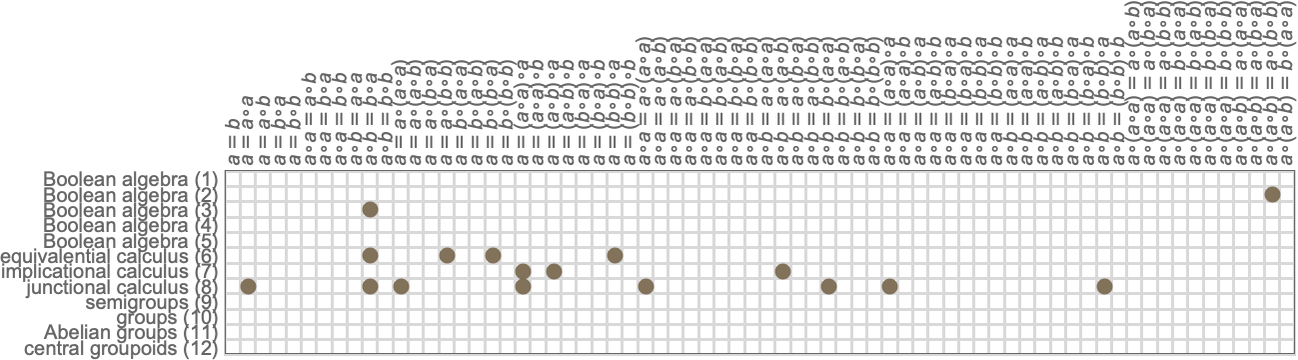
What happens if we look at entailments from these axiom systems? Eventually all theorems must show up somewhere in the entailment cone of a given axiom system. But here are the results after one step of entailment:
Some theorems have already been generated, but many have not:
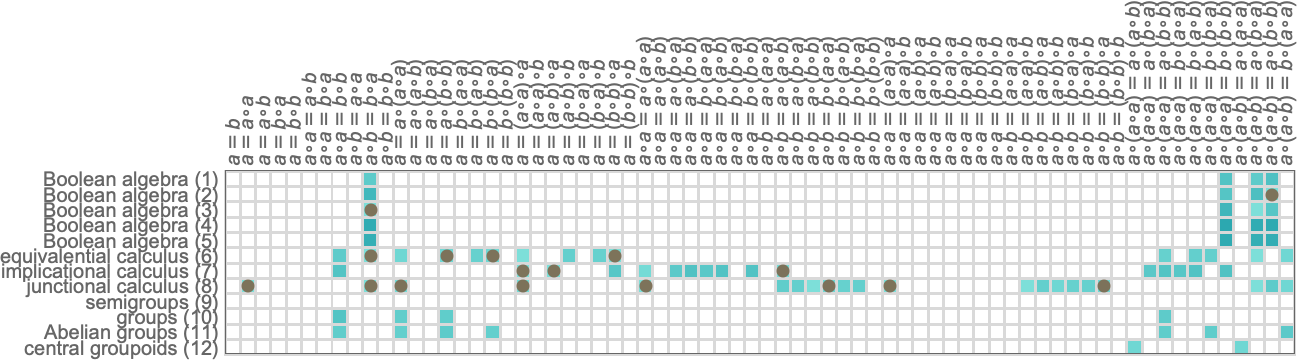
Just as we did above, we can try to “predict” theorems by constructing models. Here’s what happens if we ask what theorems hold for all valid models of size 2:
For several of the axiom systems, the models “perfectly predict” at least the theorems we show here. And for Boolean algebra, for example, this isn’t surprising: the models just correspond to identifying ∘ as Nand or Nor, and to say this gives a complete description of Boolean algebra. But in the case of groups, “size-2 models” just capture particular groups that happen to be of size 2, and for these particular groups there are special, extra theorems that aren’t true for groups in general.
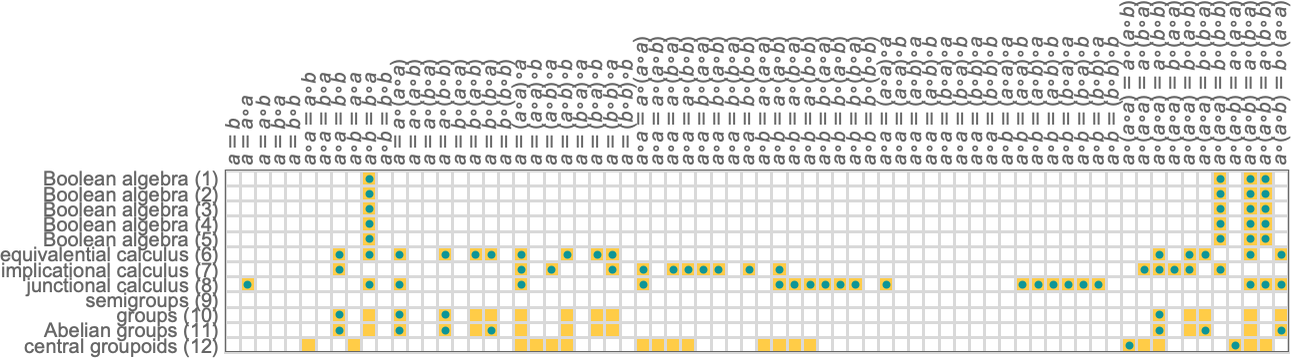
If we look at models specifically of size 3 there aren’t any examples for Boolean algebra so we don’t predict any theorems. But for group theory, for example, we start to get a slightly more accurate picture of what theorems hold in general:
Based on what we’ve seen here, is there something “obviously special” about the axiom systems that have traditionally been used in human mathematics? There are cases like Boolean algebra where the axioms in effect constrain things so much that we can reasonably say that they’re “talking about definite things” (like Nand and Nor). But there are plenty of other cases, like group theory, where the axioms provide much weaker constraints, and for example allow an infinite number of possible specific groups. But both situations occur among axiom systems “from the wild”. And in the end what we’re doing here doesn’t seem to reveal anything “obviously special” (say in the statistics of models or theorems) about “human” axiom systems.
And what this means is that we can expect that conclusions we draw from looking at the “general case of all axiom systems”—as captured in general by the ruliad—can be expected to hold in particular for the specific axiom systems and mathematical theories that human mathematics has studied.