In multiway graphs like those we’ve shown in previous sections we routinely generate very large numbers of “mathematical” expressions. But how are these expressions related to each other? And in some appropriate limit can we think of them all being embedded in some kind of “metamathematical space”?
It turns out that this is the direct analog of what in our Physics Project we call branchial space, and what in that case defines a map of the entanglements between branches of quantum history. In the mathematical case, let’s say we have a multiway graph generated using the axiom:
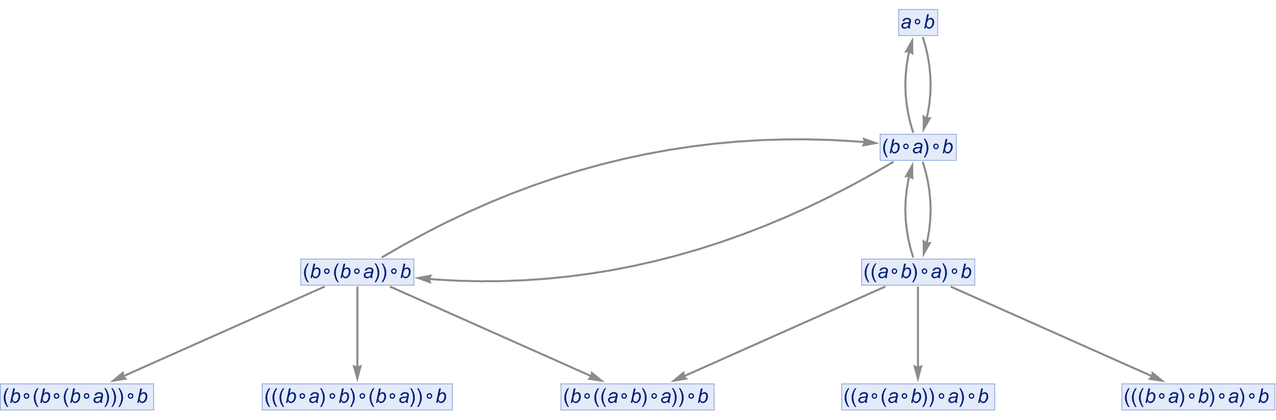
After a few steps starting from a∘b we have:
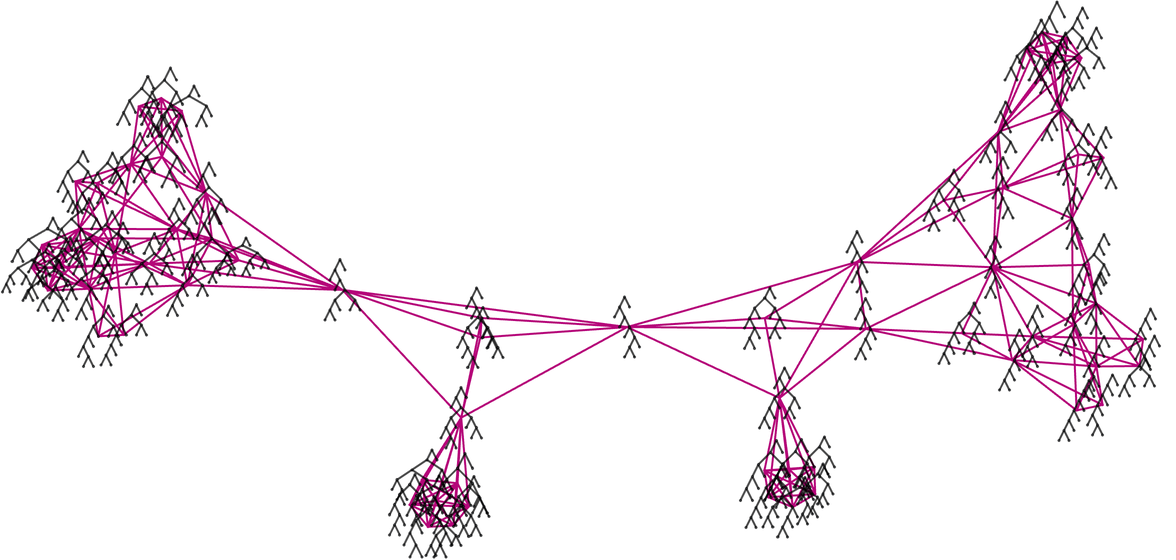
Now—just as in our Physics Project—let’s form a branchial graph by looking at the final expressions here and connecting them if they are “entangled” in the sense that they share an ancestor on the previous step:
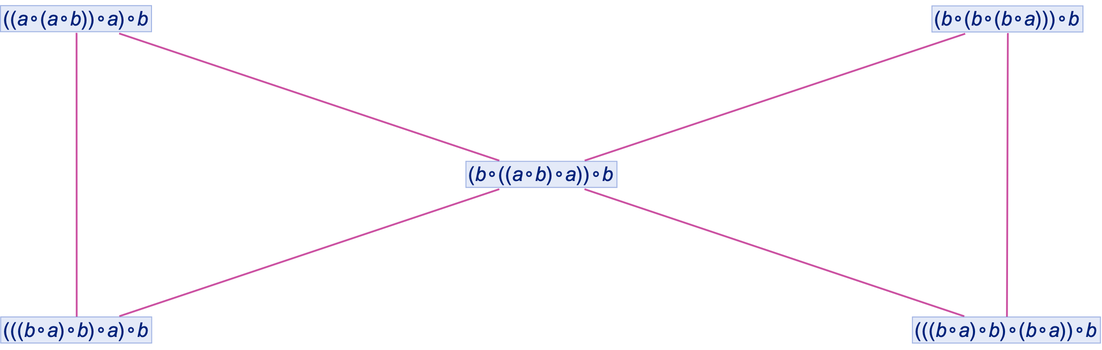
There’s some trickiness here associated with loops in the multiway graph (which are the analog of closed timelike curves in physics) and what it means to define different “steps in evolution”. But just iterating once more the construction of the multiway graph, we get a branchial graph:
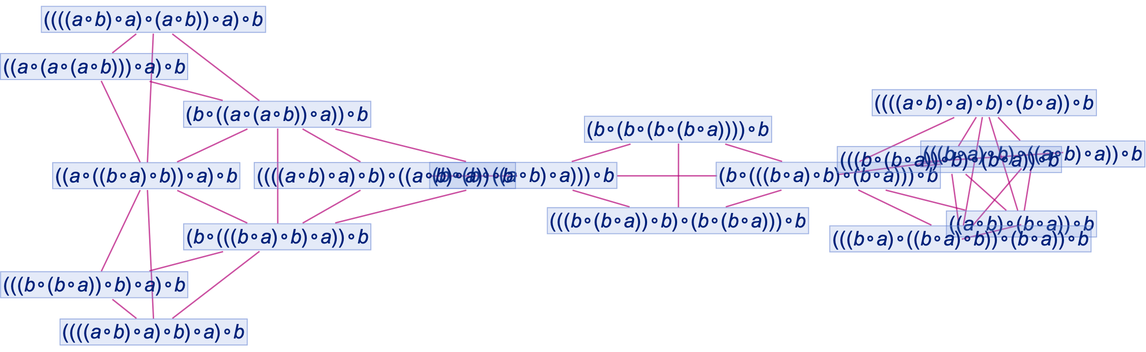
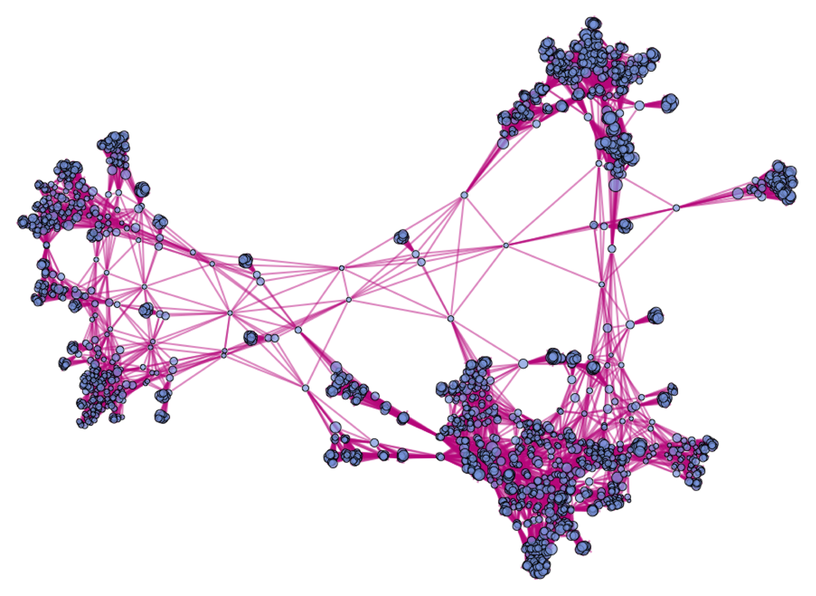
After a couple more iterations the structure of the branchial graph is (with each node sized according to the size of expression it represents):
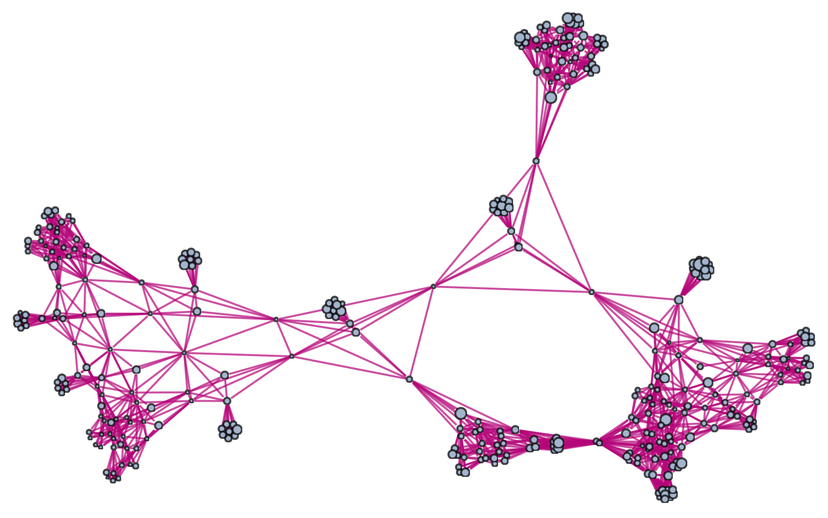
Continuing another iteration, the structure becomes:
And in essence this structure can indeed be thought of as defining a kind of “metamathematical space” in which the different expressions are embedded. But what is the “geography” of this space? This shows how expressions (drawn as trees) are laid out on a particular branchial graph
and we see that there is at least a general clustering of similar trees on the graph—indicating that “similar expressions” tend to be “nearby” in the metamathematical space defined by this axiom system.
An important feature of branchial graphs is that effects are—essentially by construction—always local in the branchial graph. For example, if one changes an expression at a particular step in the evolution of a multiway system, it can only affect a region of the branchial graph that essentially expands by one edge per step.
One can think of the affected region—in analogy with a light cone in spacetime—as being the “entailment cone” of a particular expression. The edge of the entailment cone in effect expands at a certain “maximum metamathematical speed” in metamathematical (i.e. branchial) space—which one can think of as being measured in units of “expression change per multiway step”.
By analogy with physics one can start talking in general about motion in metamathematical space. A particular proof path in the multiway graph will progressively “move around” in the branchial graph that defines metamathematical space. (Yes, there are many subtle issues here, not least the fact that one has to imagine a certain kind of limit being taken so that the structure of the branchial graph is “stable enough” to “just be moving around” in something like a “fixed background space”.)
By the way, the shortest proof path in the multiway graph is the analog of a geodesic in spacetime. And later we’ll talk about how the “density of activity” in the branchial graph is the analog of energy in physics, and how it can be seen as “deflecting” the path of geodesics, just as gravity does in spacetime.
It’s worth mentioning just one further subtlety. Branchial graphs are in effect associated with “transverse slices” of the multiway graph—but there are many consistent ways to make these slices. In physics terms one can think of the foliations that define different choices of sequences of slices as being like “reference frames” in which one is specifying a sequence of “simultaneity surfaces” (here “branchtime hypersurfaces”). The particular branchial graphs we’ve shown here are ones associated with what in physics might be called the cosmological rest frame in which every node is the result of the same number of updates since the beginning.