We’ve looked at accumulative versions of expression and string rewriting systems. So what about accumulative versions of hypergraph rewriting systems of the kind that appear in our Physics Project?
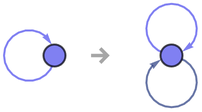
Consider the very simple hypergraph rule
or pictorially:
(Note that the nodes that are named 1 here are really like pattern variables, that could be named for example x_.)
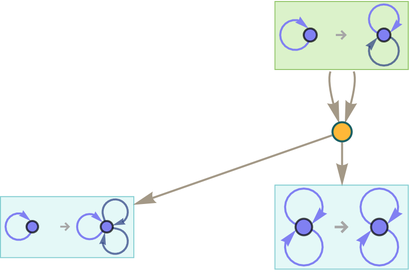
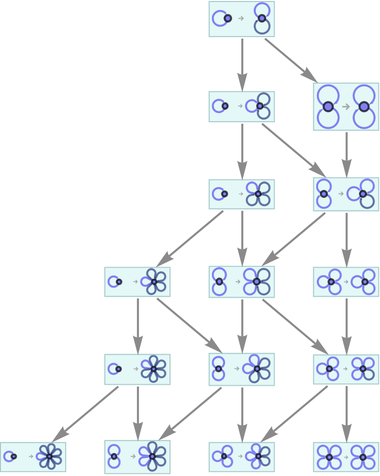
We can now do accumulative evolution with this rule, at each step combining results that involve equivalent (i.e. isomorphic) hypergraphs:
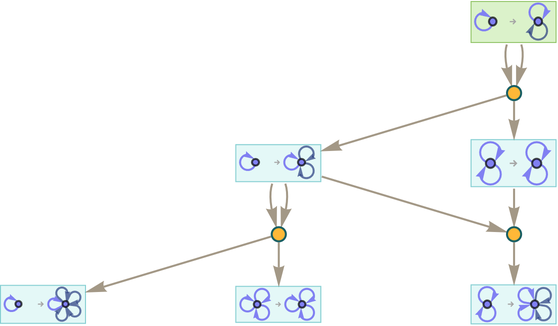
After two steps this gives:
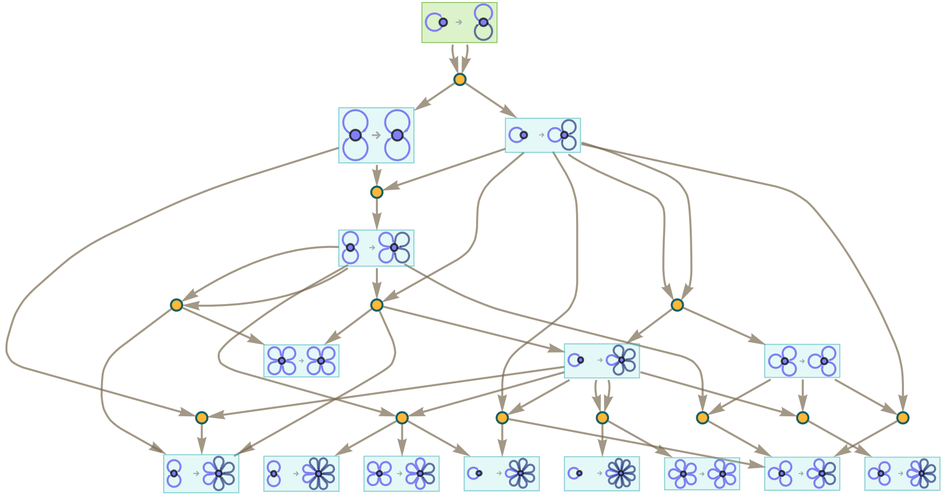
And after 3 steps:
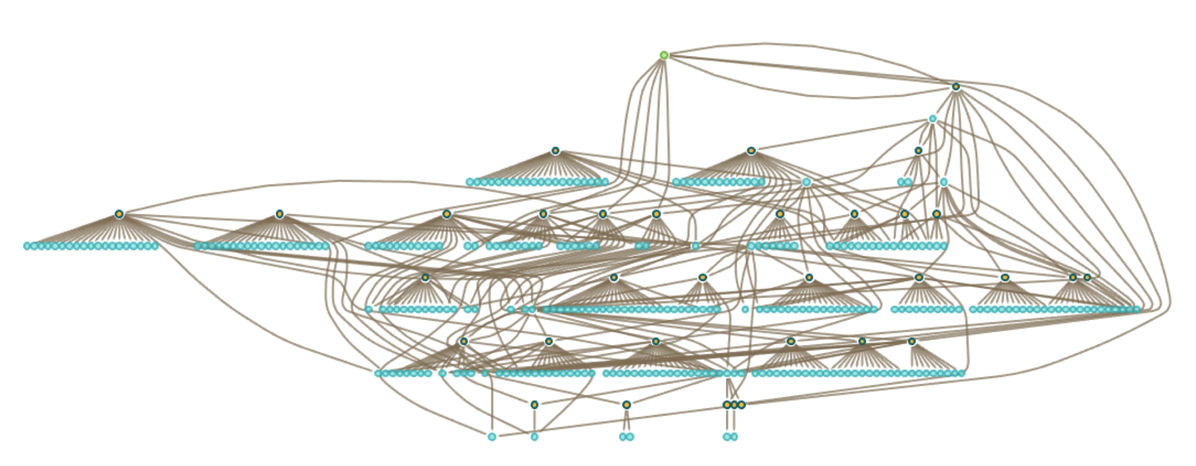
How does all this compare to “ordinary” evolution by hypergraph rewriting? Here’s a multiway graph based on applying the same underlying rule repeatedly, starting from an initial condition formed from the rule:
What we see is that the accumulative evolution in effect “shortcuts” the ordinary multiway evolution, essentially by “caching” the result of every piece of every transformation between states (which in this case are rules), and delivering a given state in fewer steps.
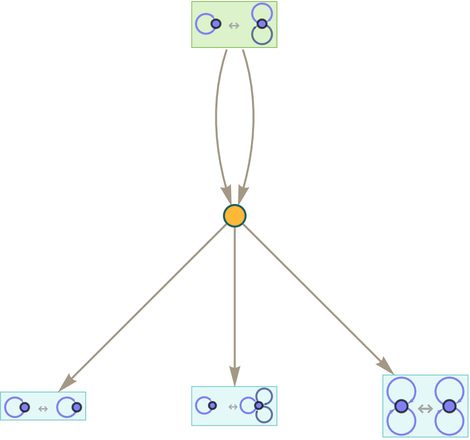
In our typical investigation of hypergraph rewriting for our Physics Project we consider one-way transformation rules. Inevitably, though, the ruliad contains rules that go both ways. And here, in an effort to understand the correspondence with our metamodel of mathematics, we can consider two-way hypergraph rewriting rules. An example is the two-way version of the rule above:
Now the token-event graph becomes
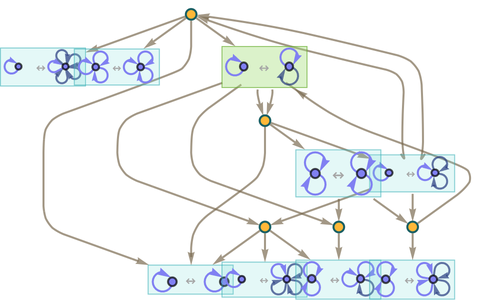
or after 2 steps (where now the transformations from “later states” to “earlier states” have started to fill in):
Just like in ordinary hypergraph evolution, the only way to get hypergraphs with additional hyperedges is to start with a rule that involves the addition of new hyperedges—and the same is true for the addition of new elements. Consider the rule:
After 1 step this gives
while after 2 steps it gives:
The general appearance of this token-event graph is not much different from what we saw with string rewrite or expression rewrite systems. So what this suggests is that it doesn’t matter much whether we’re starting from our metamodel of axiomatic mathematics or from any other reasonably rich rewriting system: we’ll always get the same kind of “large-scale” token-event graph structure. And this is an example of what we’ll use to argue for general laws of metamathematics.