In the typical practice of pure mathematics the main objective is to establish theorems. Yes, one wants to know that a theorem has a proof (and perhaps the proof will be helpful in understanding the theorem), but the main focus is on theorems and not on proofs. In our effort to “go underneath” mathematics, however, we want to study not only what theorems there are, but also the process by which the theorems are reached. We can view it as an important simplifying assumption of typical mathematical observers that all that matters is theorems—and that different proofs aren’t relevant. But to explore the underlying structure of metamathematics, we need to unpack this—and in effect look directly at the structure of proof space.
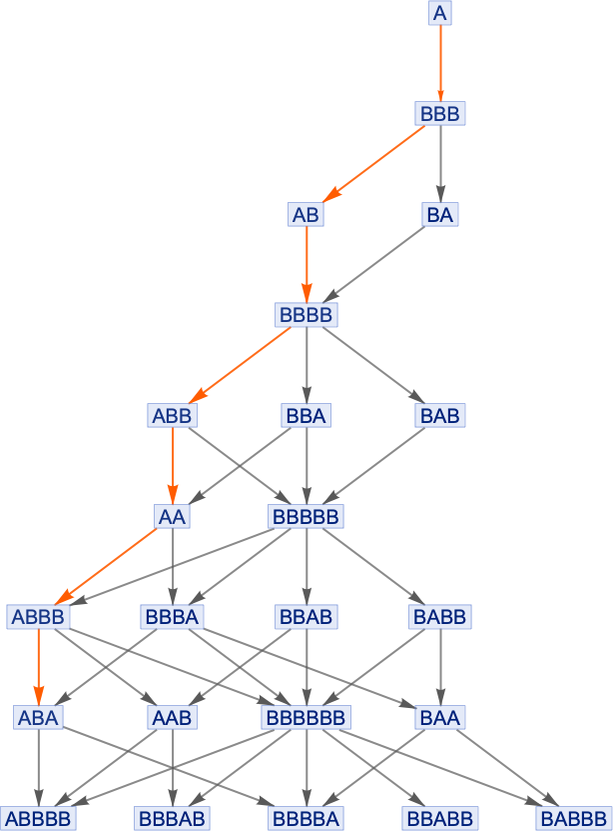
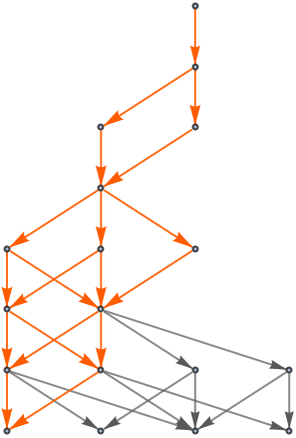
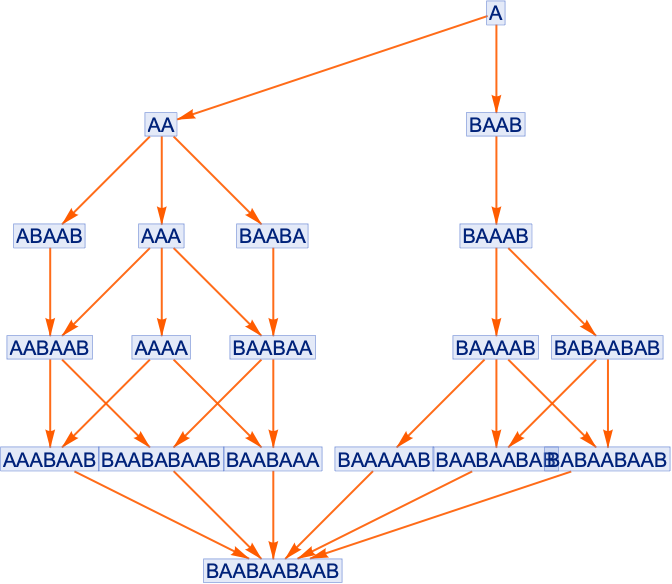
Let’s consider a simple system based on strings. Say we have the rewrite rule {ABBB,BBA} and we want to establish the theorem AABA. To do this we have to find some path from A to ABA in the multiway system (or, effectively, in the entailment cone for this axiom system):
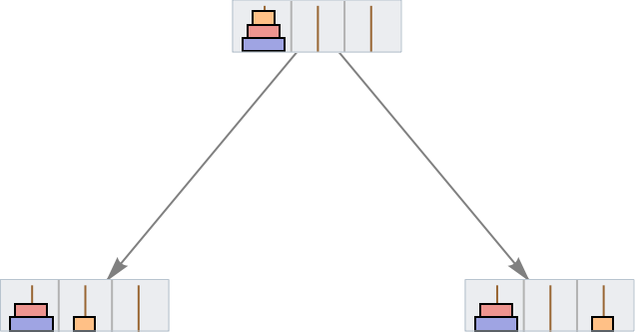
But this isn’t the only possible path, and thus the only possible proof. In this particular case, there are 20 distinct paths, each corresponding to at least a slightly different proof:
But one feature here is that all these different proofs can in a sense be “smoothly deformed” into each other, in this case by progressively changing just one step at a time. So this means that in effect there is no nontrivial topology to proof space in this case—and “distinctly inequivalent” collections of proofs:
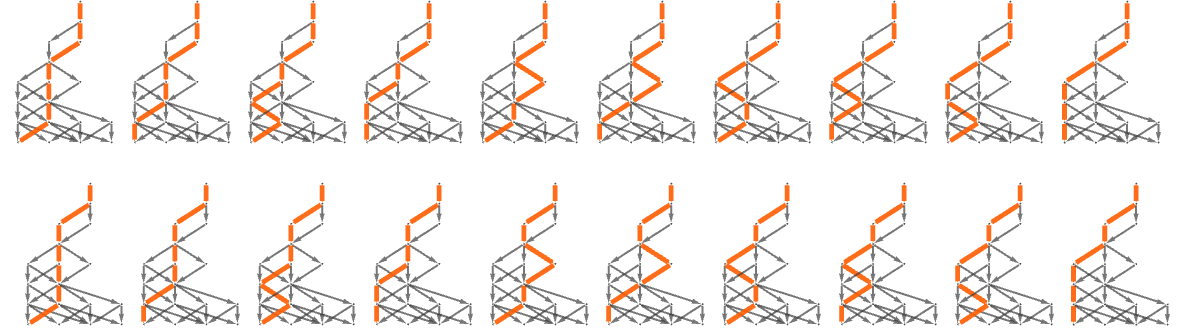
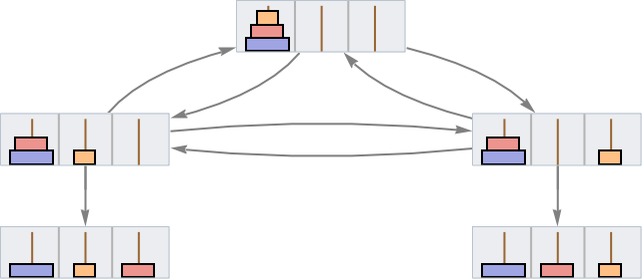
But consider instead the rule {AAA,ABAAB}. With this “axiom system” there are 15 possible proofs for the theorem ABAABAABAAB:
Pulling out just the proofs we get:
And we see that in a sense there’s a “hole” in proof space here—so that there are two distinctly different kinds of proofs that can be done.
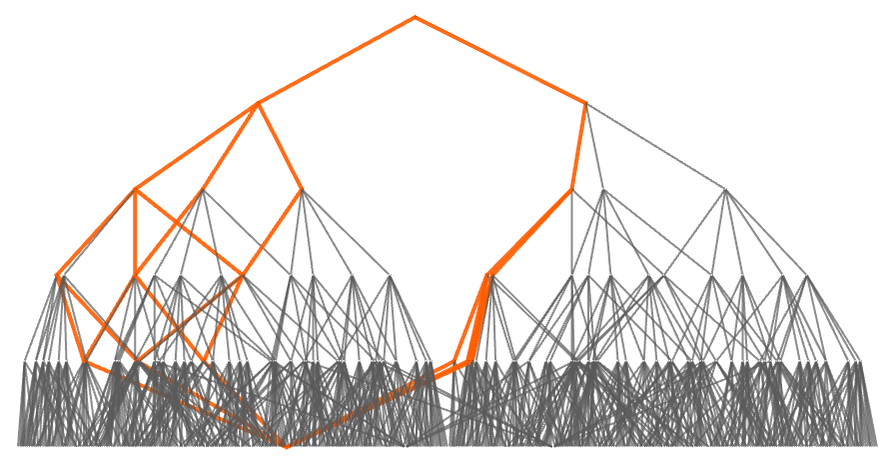
After 2 steps we have:
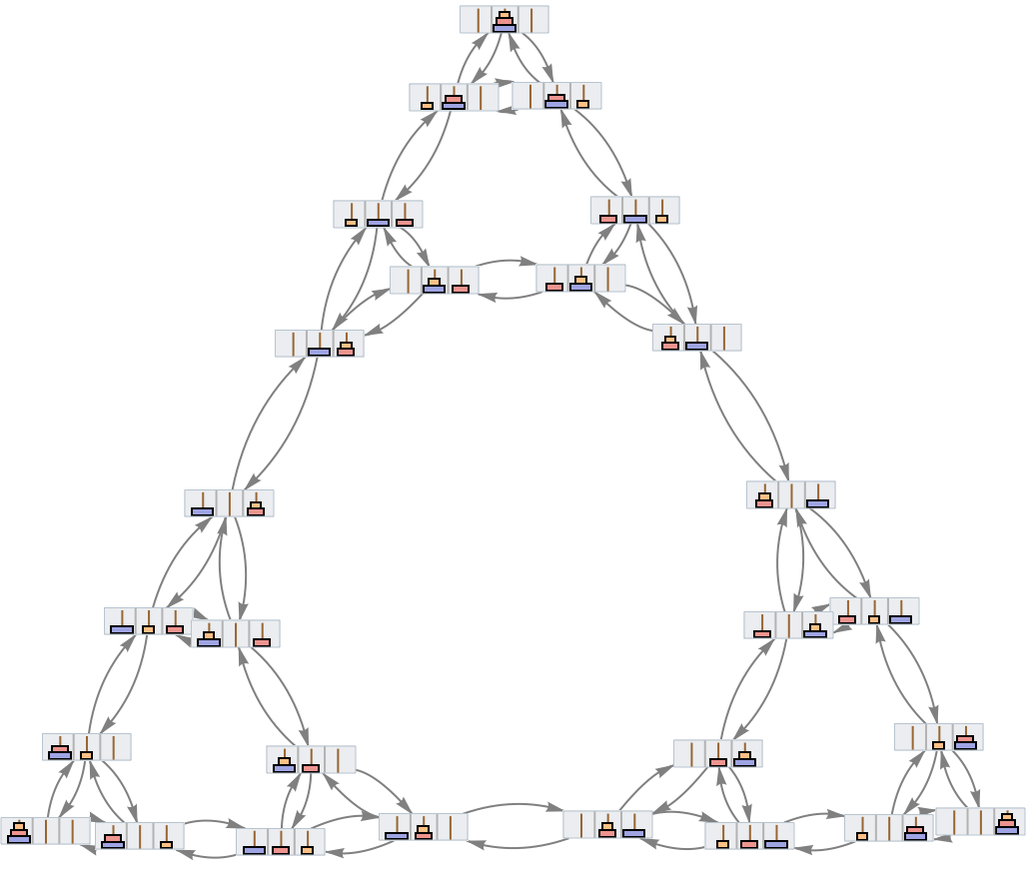
And after 8 steps (in this case) we have the whole “game graph”:
The corresponding result for 4 disks is:
And in each case we see the phenomenon of nontrivial topology. What fundamentally causes this? In a sense it reflects the possibility for distinctly different strategies that lead to the same result. Here, for example, different sides of the “main loop” correspond to the “foundational choice” of whether to move the biggest disk first to the left or to the right. And the same basic thing happens with 4 disks on 4 pegs, though the overall structure is more complicated there:
If two paths diverge in a multiway system it could be that it will never be possible for them to merge again. But whenever the system has the property of confluence, it’s guaranteed that eventually the paths will merge. And, as it turns out, our accumulative evolution setup guarantees that (at least ignoring generation of new variables) confluence will always be achieved. But the issue is how quickly. If branches always merge after just one step, then in a sense there’ll always be topologically trivial proof space. But if the merging can take awhile (and in a continuum limit, arbitrarily long) then there’ll in effect be nontrivial topology.
And one consequence of the nontrivial topology we’re discussing here is that it leads to disconnection in branchial space. Here are the branchial graphs for the first 3 steps in our original 3-disk 3-peg case:
For the first two steps, the branchial graphs stay connected; but on the third step there’s disconnection. For the 4-disk 4-peg case the sequence of branchial graphs begins:
At the beginning (and also the end) there’s a single component, that we might think of as a coherent region of metamathematical space. But in the middle it breaks into multiple disconnected components—in effect reflecting the emergence of multiple distinct regions of metamathematical space with something like event horizons temporarily existing between them.
How should we interpret this? First and foremost, it’s something that reveals that there’s structure “below” the “fluid dynamics” level of mathematics; it’s something that depends on the discrete “axiomatic infrastructure” of metamathematics. And from the point of view of our Physics Project, we can think of it as a kind of metamathematical analog of a “quantum effect”.
In our Physics Project we imagine different paths in the multiway system to correspond to different possible quantum histories. The observer is in effect spread over multiple paths, which they coarse grain or conflate together. An “observable quantum effect” occurs when there are paths that can be followed by the system, but that are somehow “too far apart” to be immediately coarse-grained together by the observer.
Put another way, there is “noticeable quantum interference” when the different paths corresponding to different histories that are “simultaneously happening” are “far enough apart” to be distinguished by the observer. “Destructive interference” is presumably associated with paths that are so far apart that to conflate them would effectively require conflating essentially every possible path. (And our later discussion of the relationship between falsity and the “principle of explosion” then suggests a connection between destructive interference in physics and falsity in mathematics.)
In essence what determines the extent of “quantum effects” is then our “size” as observers in branchial space relative to the size of features in branchial space such as the “topological holes” we’ve been discussing. In the metamathematical case, the “size” of us as observers is in effect related to our ability (or choice) to distinguish slight differences in axiomatic formulations of things. And what we’re saying here is that when there is nontrivial topology in proof space, there is an intrinsic dynamics in metamathematical entailment that leads to the development of distinctions at some scale—though whether these become “visible” to us as mathematical observers depends on how “strong a metamathematical microscope” we choose to use relative to the scale of the “topological holes”.