Now that we’ve finished describing the many technical issues involved in constructing our metamodel of mathematics, we can start looking at its consequences. We discussed above how multiway graphs formed from expressions can be used to define a branchial graph that represents a kind of “metamathematical space”. We can now use a similar approach to set up a metamathematical space for our full metamodel of the “progressive accumulation” of mathematical statements.
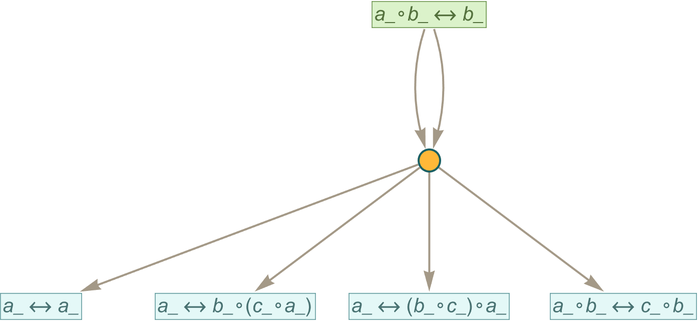
Let’s start by ignoring cosubstitution and bisubstitution and considering only the process of substitution—and beginning with the axiom:
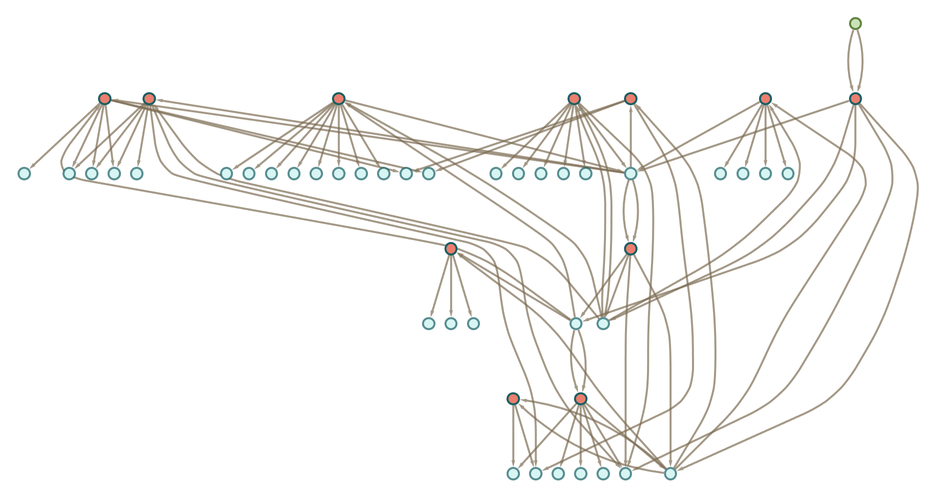
Doing accumulative evolution from this axiom we get the token-event graph
or after 2 steps:
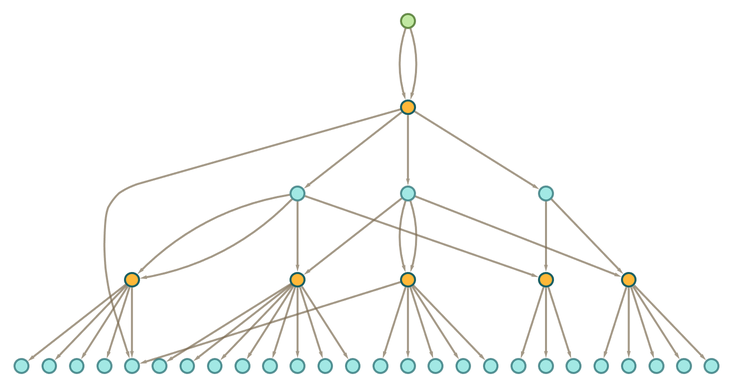
From this we can derive an “effective multiway graph” by directly connecting all input and output tokens involved in each event:
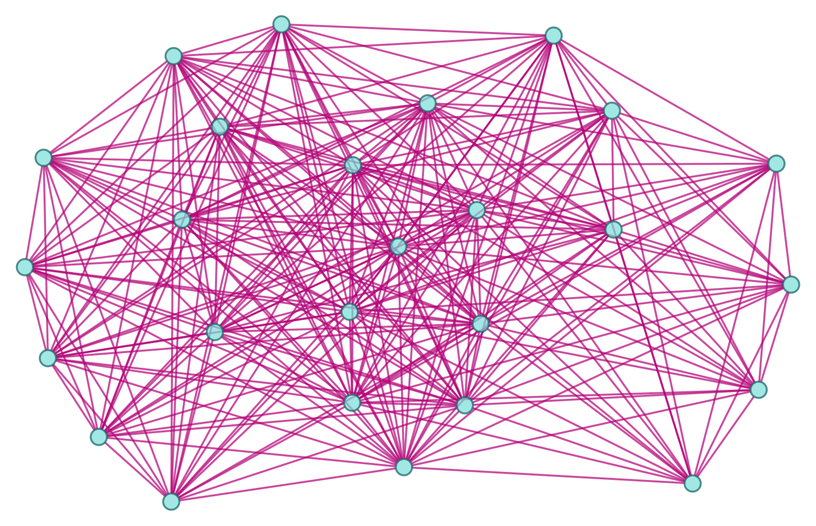
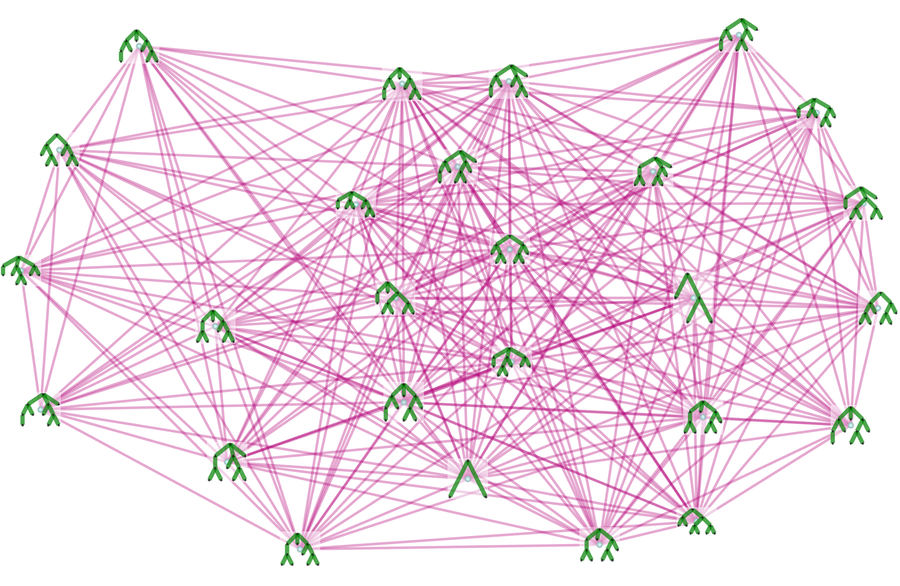
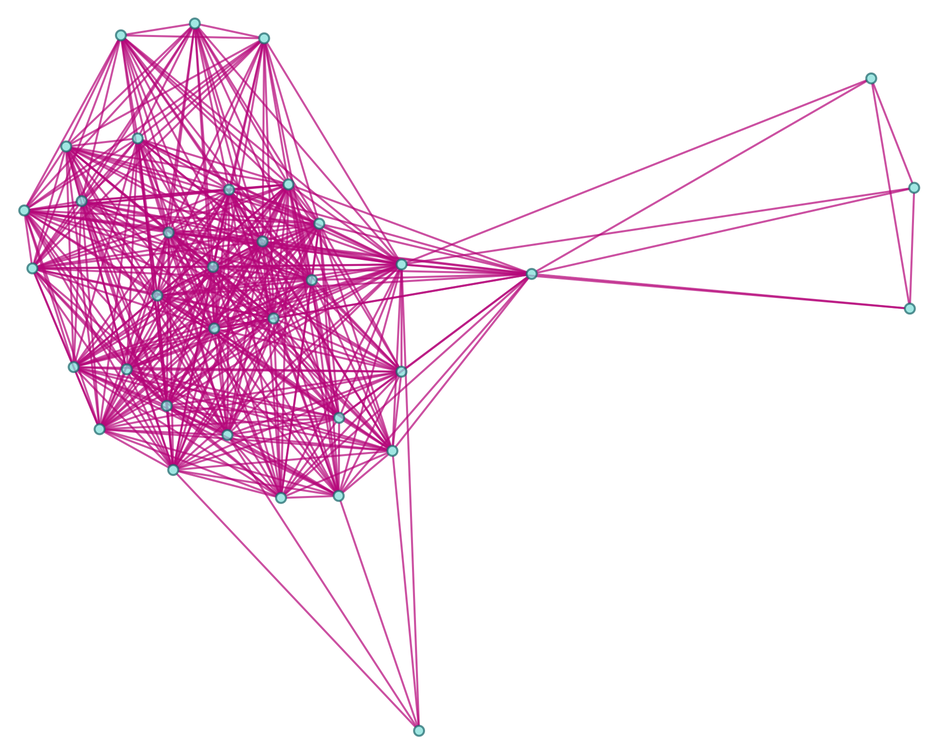
And then we can produce a branchial graph, which in effect yields an approximation to the “metamathematical space” generated by our axiom:
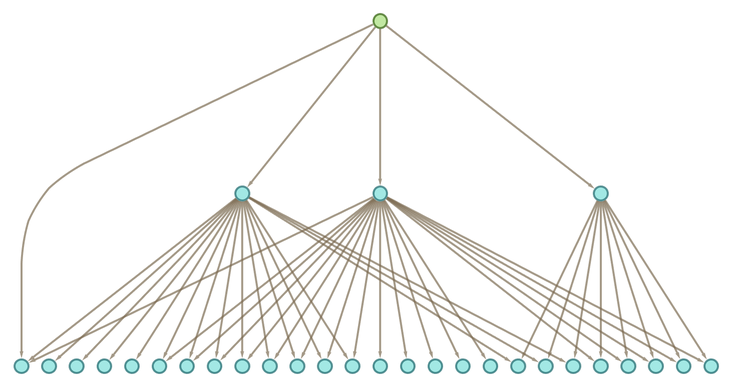
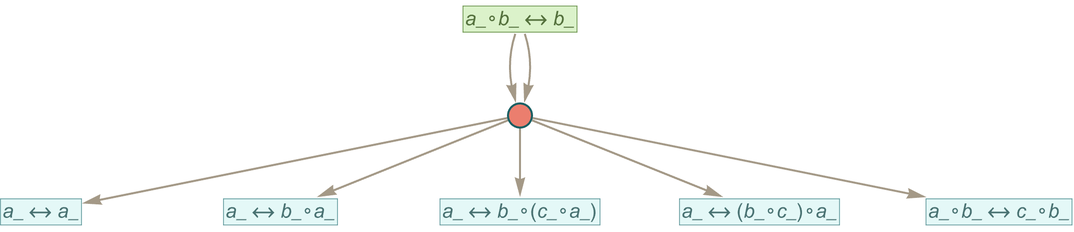
Showing the statements produced in the form of trees we get (with the top node representing ↔):
If we do the same thing with full bisubstitution, then even after one step we get a slightly larger token-event graph:
After two steps, we get
which contains 46 statements, compared to 42 if only substitution is used. The corresponding branchial graph is:
The adjacency matrices for the substitution and bisubstitution cases are then
which have 80% and 85% respectively of the number of edges in complete graphs of these sizes.
Branchial graphs are usually quite dense, but they nevertheless do show definite structure. Here are some results after 2 steps: