A fundamental feature of our metamodel of mathematics is the idea that a given set of mathematical statements can entail others. But in this picture what does “mathematical progress” look like?
In analogy with physics one might imagine it would be like the evolution of the universe through time. One would start from some limited set of axioms and then—in a kind of “mathematical Big Bang”—these would lead to a progressively larger entailment cone containing more and more statements of mathematics. And in analogy with physics, one could imagine that the process of following chains of successive entailments in the entailment cone would correspond to the passage of time.
But realistically this isn’t how most of the actual history of human mathematics has proceeded. Because people—and even their computers—basically never try to extend mathematics by axiomatically deriving all possible valid mathematical statements. Instead, they come up with particular mathematical statements that for one reason or another they think are valid and interesting, then try to prove these.
Sometimes the proof may be difficult, and may involve a long chain of entailments. Occasionally—especially if automated theorem proving is used—the entailments may approximate a geodesic path all the way from the axioms. But the practical experience of human mathematics tends to be much more about identifying “nearby statements” and then trying to “fit them together” to deduce the statement one’s interested in.
And in general human mathematics seems to progress not so much through the progressive “time evolution” of an entailment graph as through the assembly of what one might call an “entailment fabric” in which different statements are being knitted together by entailments.
In physics, the analog of the entailment graph is basically the causal graph which builds up over time to define the content of a light cone (or, more accurately, an entanglement cone). The analog of the entailment fabric is basically the (more-or-less) instantaneous state of space (or, more accurately, branchial space).
In our Physics Project we typically take our lowest-level structure to be a hypergraph—and informally we often say that this hypergraph “represents the structure of space”. But really we should be deducing the “structure of space” by taking a particular time slice from the “dynamic evolution” represented by the causal graph—and for example we should think of two “atoms of space” as “being connected” in the “instantaneous state of space” if there’s a causal connection between them defined within the slice of the causal graph that occurs within the time slice we’re considering. In other words, the “structure of space” is knitted together by the causal connections represented by the causal graph. (In traditional physics, we might say that space can be “mapped out” by looking at overlaps between lots of little light cones.)
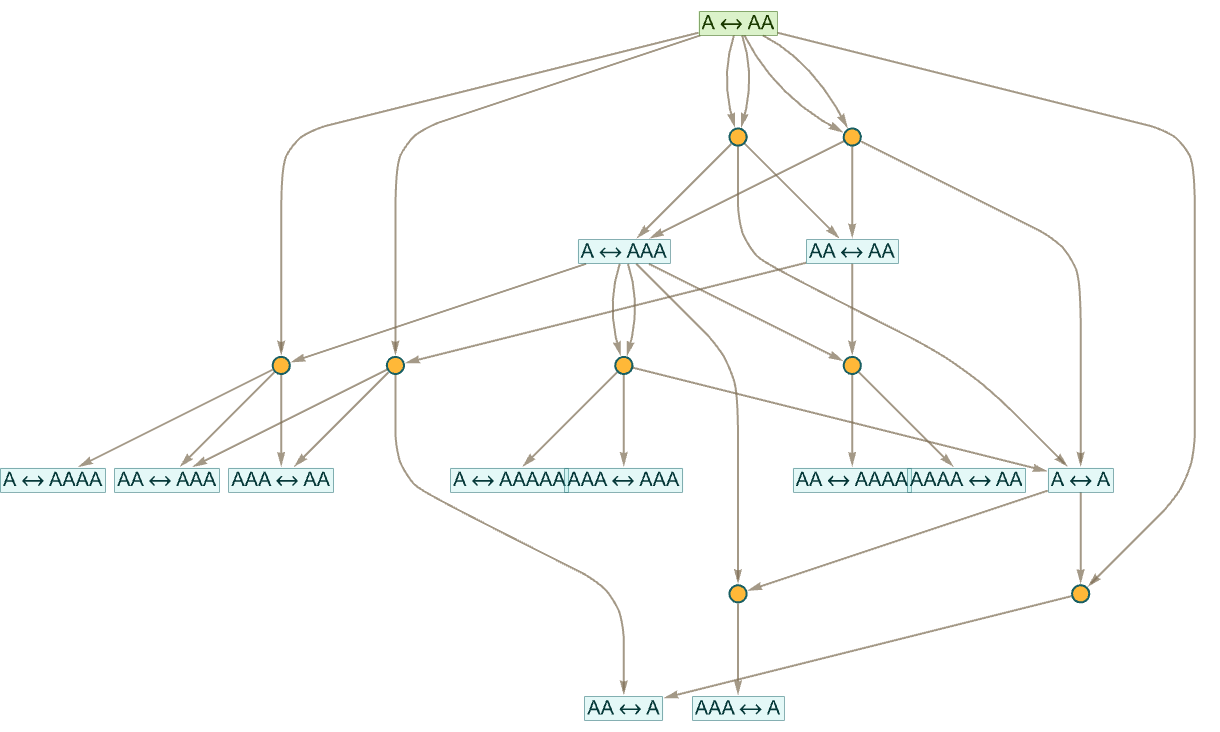
Let’s look at how this works out in our metamathematical setting, using string rewrites to simplify things. If we start from the axiom AAA this is the beginning of the entailment cone it generates:
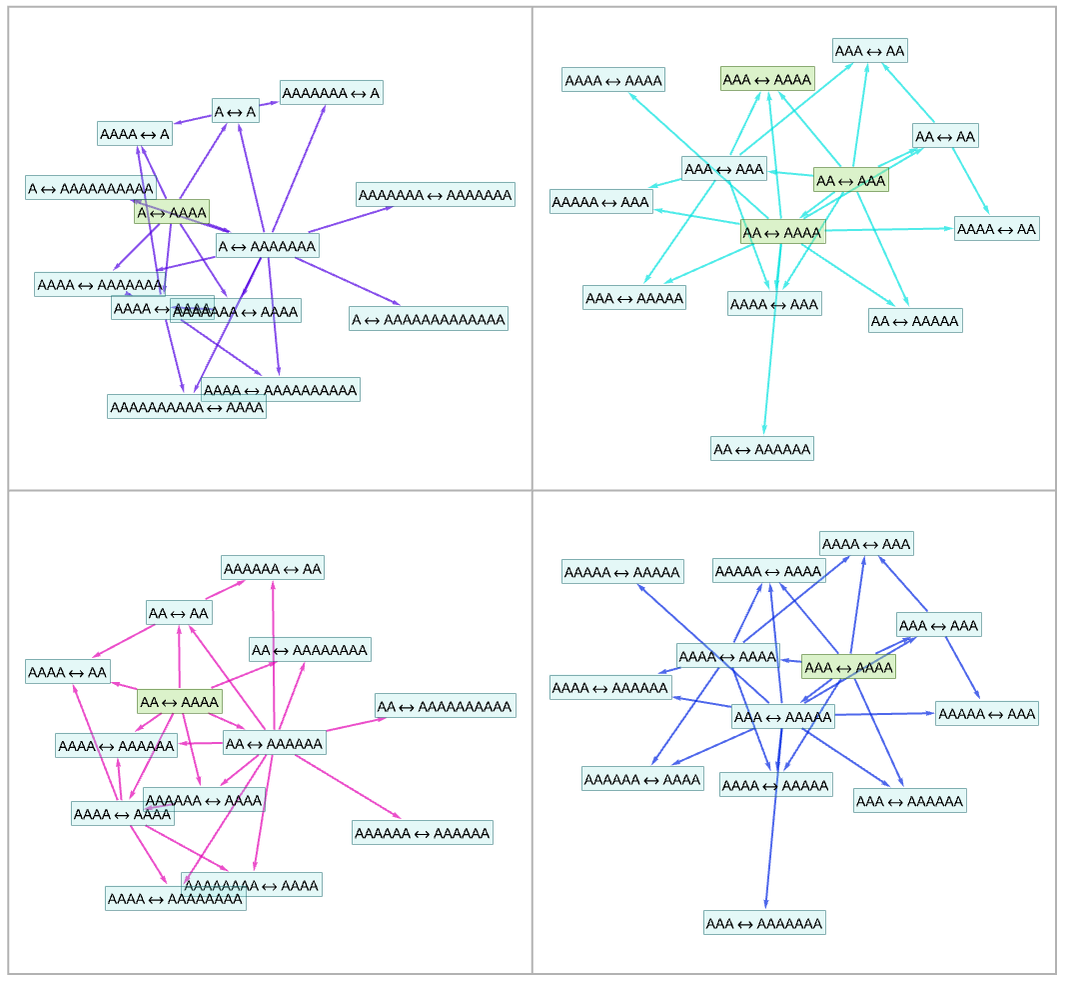
But instead of starting with one axiom and building up a progressively larger entailment cone, let’s start with multiple statements, and from each one generate a small entailment cone, say applying each rule at most twice. Here are entailment cones started from several different statements:
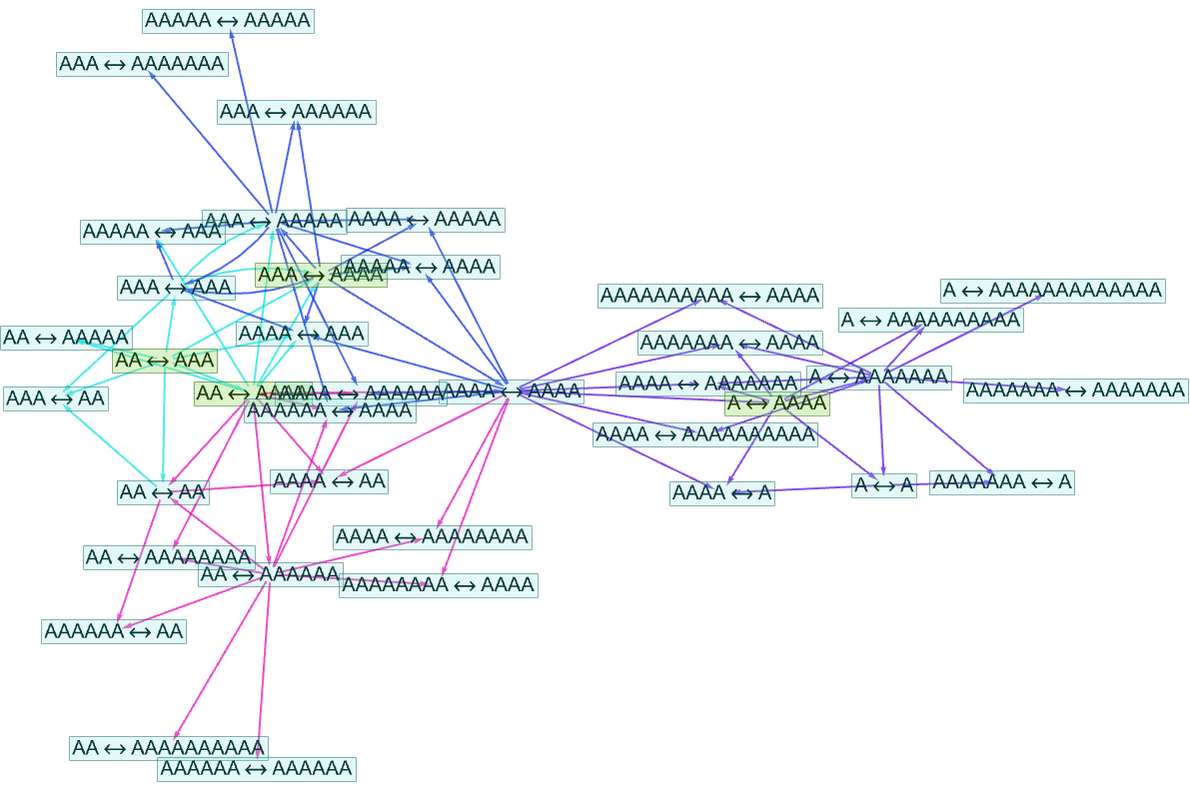
But the crucial point is that these entailment cones overlap—so we can knit them together into an “entailment fabric”:
Or with more pieces and another step of entailment:
And in a sense this is a “timeless” way to imagine building up mathematics—and metamathematical space. Yes, this structure can in principle be viewed as part of the branchial graph obtained from a slice of an entailment graph (and technically this will be a useful way to think about it). But a different view—closer to the practice of human mathematics—is that it’s a “fabric” formed by fitting together many different mathematical statements. It’s not something where one’s tracking the overall passage of time, and seeing causal connections between things—as one might in “running a program”. Rather, it’s something where one’s fitting pieces together in order to satisfy constraints—as one might in creating a tiling.
Underneath everything is the ruliad. And entailment cones and entailment fabrics can be thought of just as different samplings or slicings of the ruliad. The ruliad is ultimately the entangled limit of all possible computations. But one can think of it as being built up by starting from all possible rules and initial conditions, then running them for an infinite number of steps. An entailment cone is essentially a “slice” of this structure where one’s looking at the “time evolution” from a particular rule and initial condition. An entailment fabric is an “orthogonal” slice, looking “at a particular time” across different rules and initial conditions. (And, by the way, rules and initial conditions are essentially equivalent, particularly in an accumulative system.)
One can think of these different slices of the ruliad as being what different kinds of observers will perceive within the ruliad. Entailment cones are essentially what observers who persist through time but are localized in rulial space will perceive. Entailment fabrics are what observers who ignore time but explore more of rulial space will perceive.
Elsewhere I’ve argued that a crucial part of what makes us perceive the laws of physics we do is that we are observers who consider ourselves to be persistent through time. But now we’re seeing that in the way human mathematics is typically done, the “mathematical observer” will be of a different character. And whereas for a physical observer what’s crucial is causality through time, for a mathematical observer (at least one who’s doing mathematics the way it’s usually done) what seems to be crucial is some kind of consistency or coherence across metamathematical space.
In physics it’s far from obvious that a persistent observer would be possible. It could be that with all those detailed computationally irreducible processes happening down at the level of atoms of space there might be nothing in the universe that one could consider consistent through time. But the point is that there are certain “coarse-grained” attributes of the behavior that are consistent through time. And it is by concentrating on these that we end up describing things in terms of the laws of physics we know.
There’s something very analogous going on in mathematics. The detailed branchial structure of metamathematical space is complicated, and presumably full of computational irreducibility. But once again there are “coarse-grained” attributes that have a certain consistency and coherence across it. And it is on these that we concentrate as human “mathematical observers”. And it is in terms of these that we end up being able to do “human-level mathematics”—in effect operating at a “fluid dynamics” level rather than a “molecular dynamics” one.
The possibility of “doing physics in the ruliad” depends crucially on the fact that as physical observers we assume that we have certain persistence and coherence through time. The possibility of “doing mathematics (the way it’s usually done) in the ruliad” depends crucially on the fact that as “mathematical observers” we assume that the mathematical statements we consider will have a certain coherence and consistency—or, in effect, that it’s possible for us to maintain and grow a coherent body of mathematical knowledge, even as we try to include all sorts of new mathematical statements.