experiments, then one quickly finds that even rather simple systems based on numbers can lead to highly complex behavior.
But what is the origin of this complexity? And how does it relate to the complexity we have seen in systems like cellular automata?
One might think that with all the mathematics developed for studying systems based on numbers it would be easy to answer these kinds of questions. But in fact traditional mathematics seems for the most part to lead to more confusion than help.
One basic problem is that numbers are handled very differently in traditional mathematics from the way they are handled in computers and computer programs. For in a sense, traditional mathematics makes a fundamental idealization: it assumes that numbers are elementary objects whose only relevant attribute is their size. But in a computer, numbers are not elementary objects. Instead, they must be represented explicitly, typically by giving a sequence of digits.
The idea of representing a number by a sequence of digits is familiar from everyday life: indeed, our standard way of writing numbers corresponds exactly to giving their digit sequences in base 10. What base 10 means is that for each digit there are 10 possible choices:
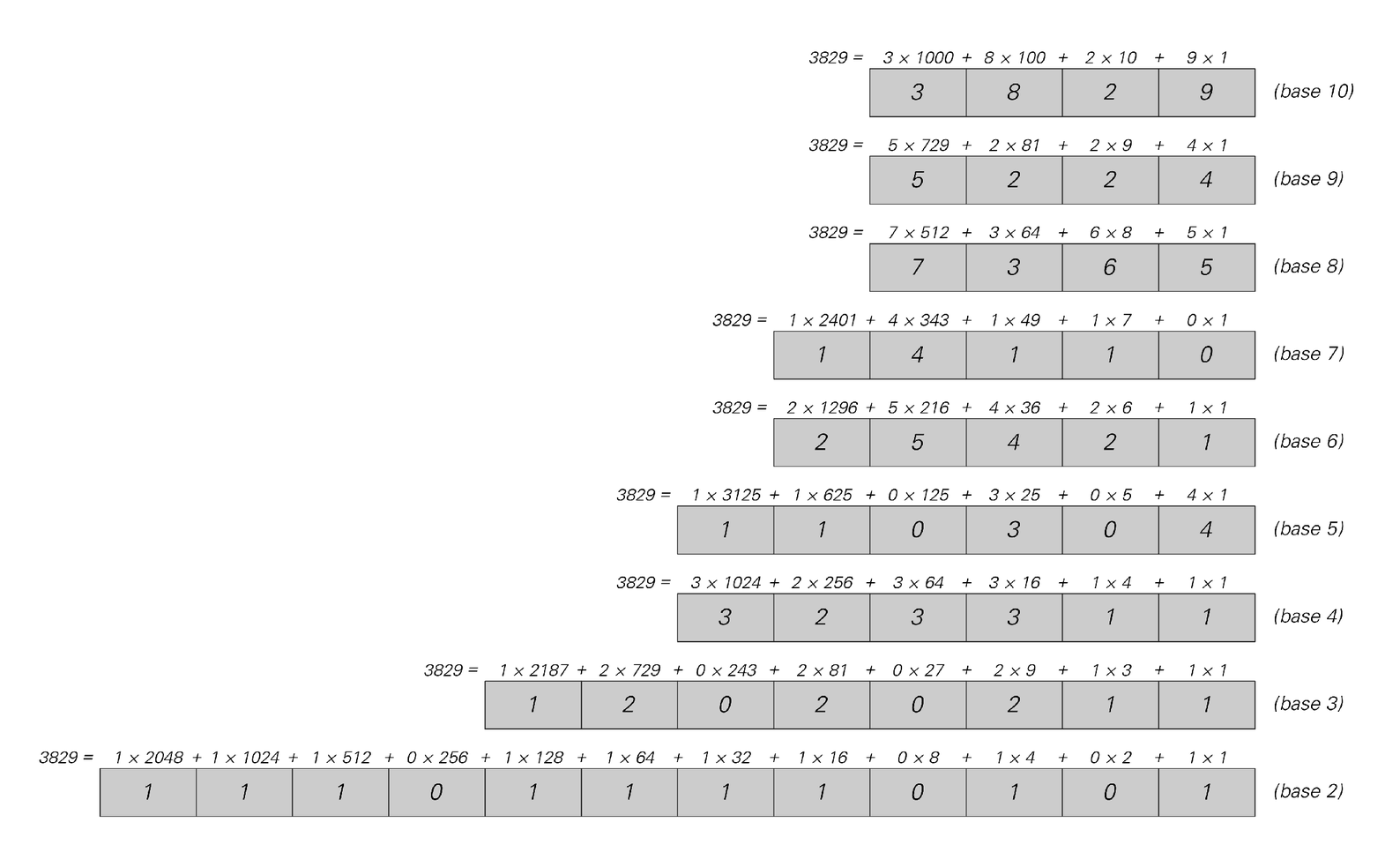
Representations of the number 3829 in various bases. The most familiar case is base 10, where starting from the right successive digits correspond to units, tens, hundreds and so on. In base 10, there are 10 possible digits: 0 through 9. In other bases, there are a different number of possible digits. In base 2, as used in practical computers, there are just two possible digits: 0 and 1. And in this base, successive digits starting from the right have coefficients 1, 2, 4 = 2×2, 8 = 2×2×2, etc.



