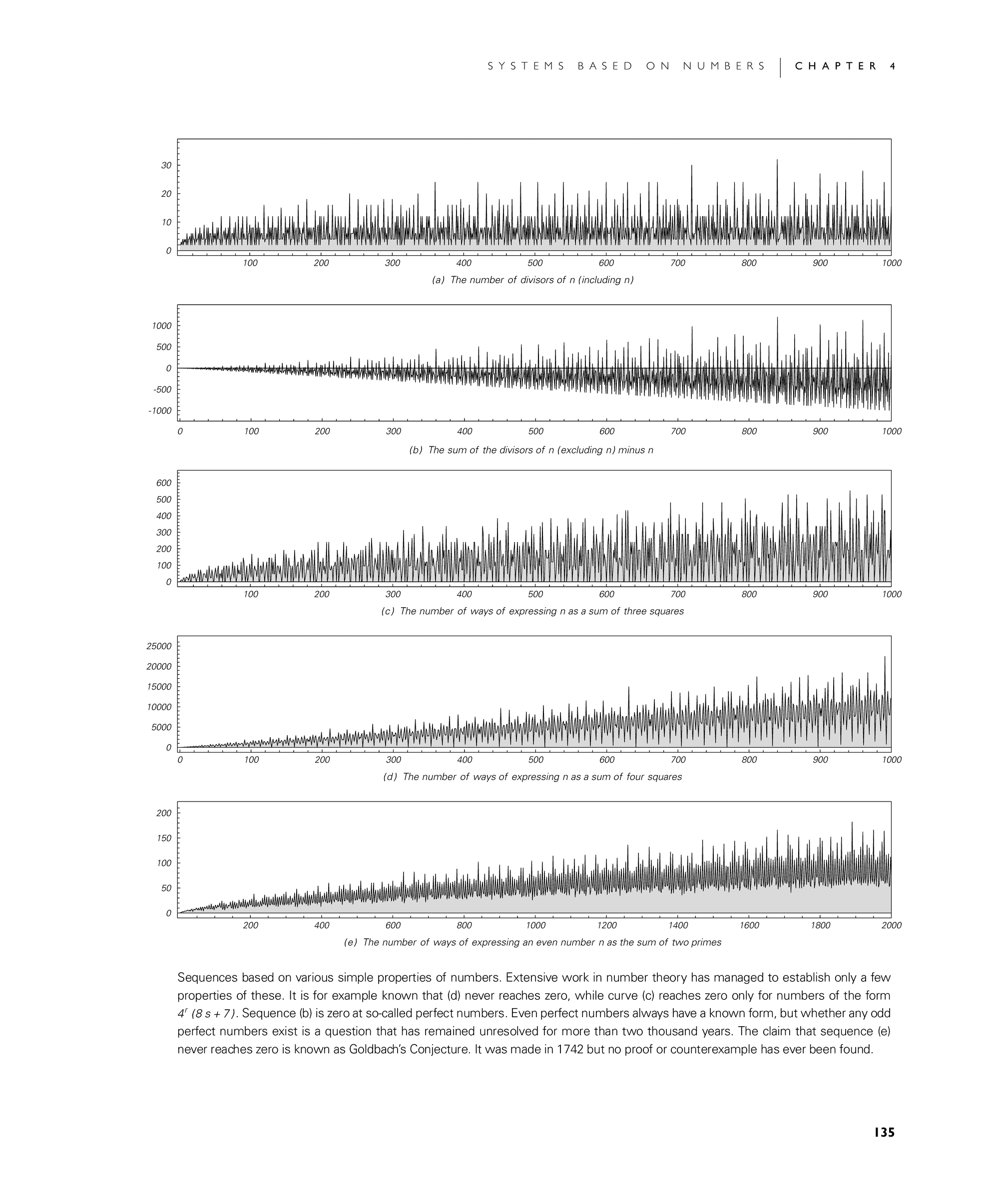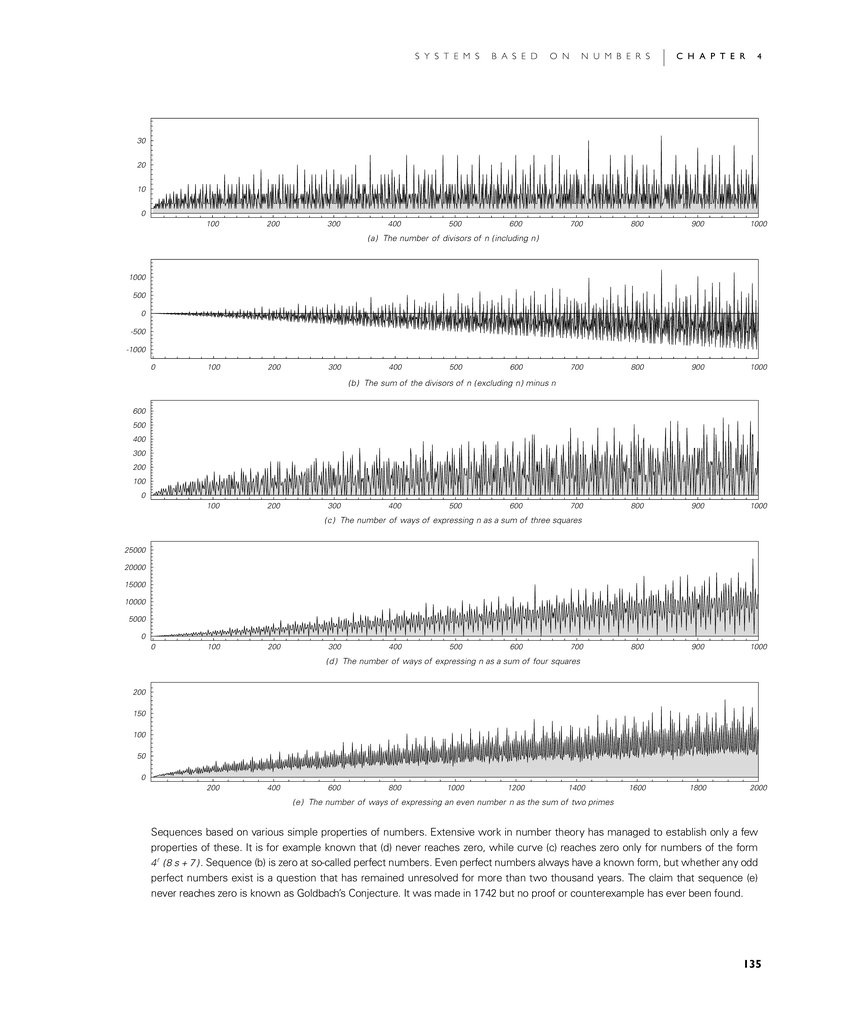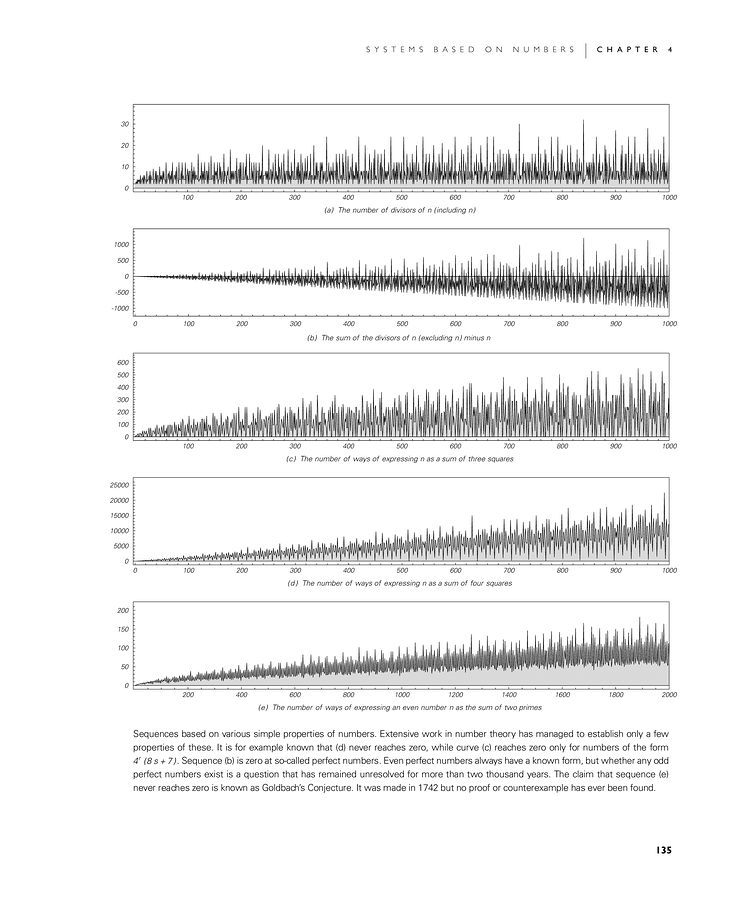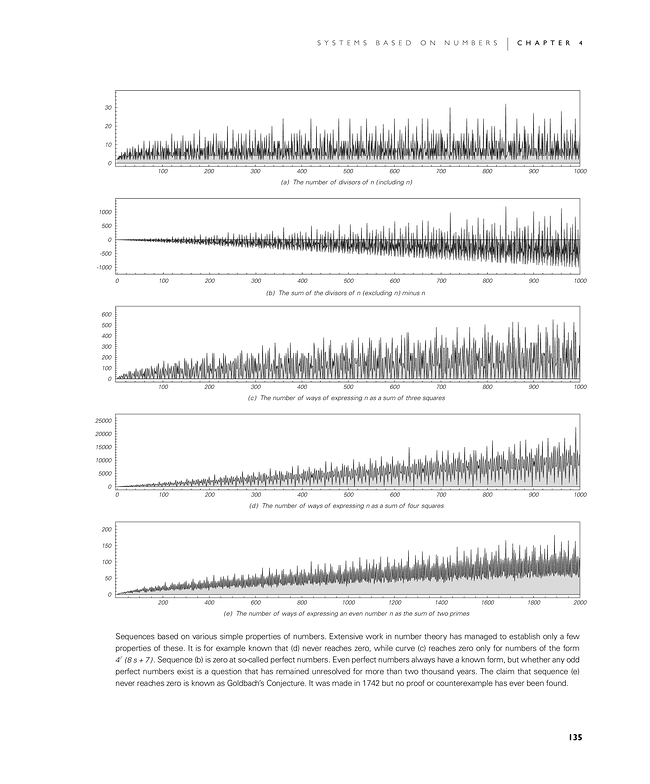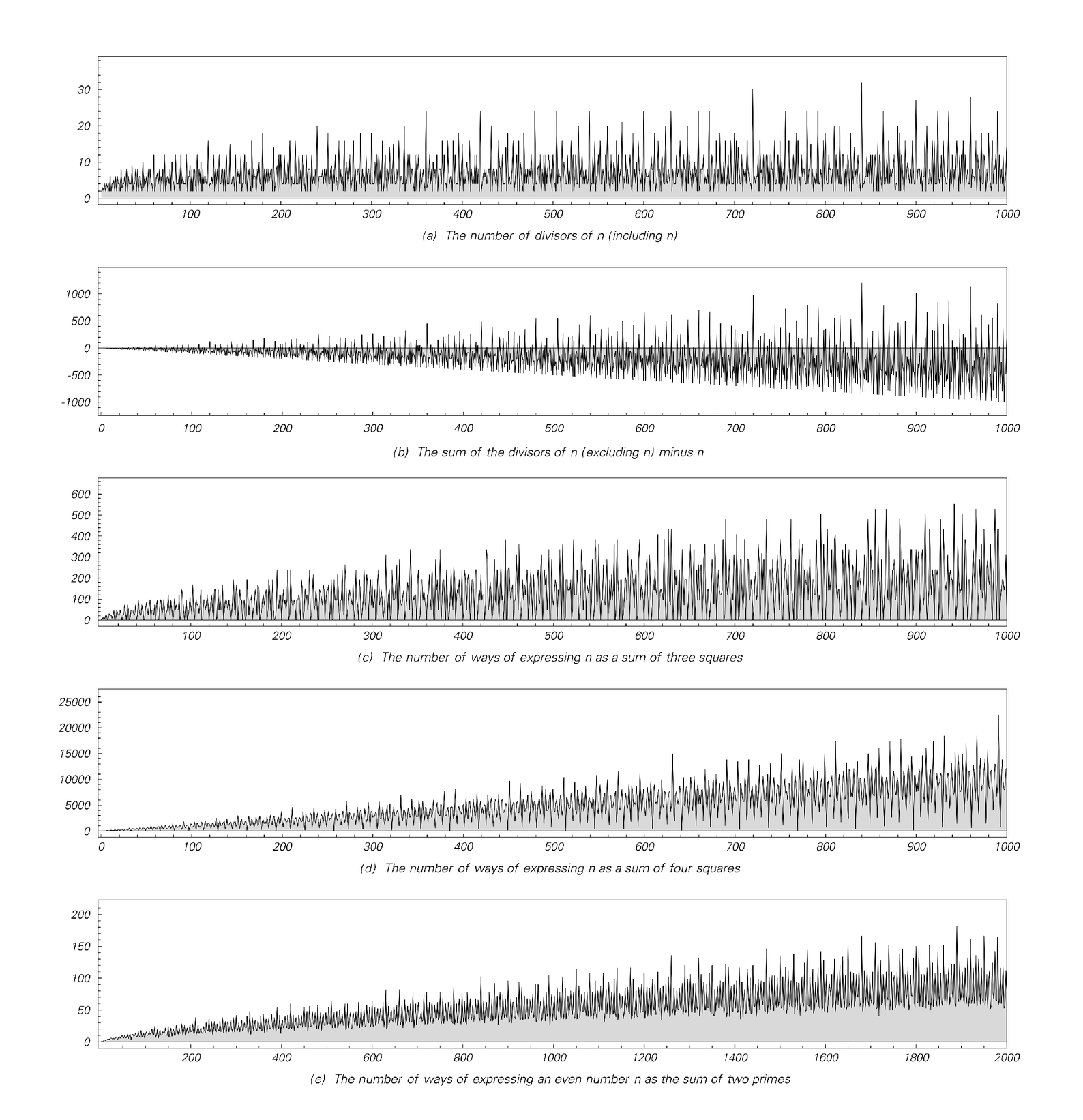
Sequences based on various simple properties of numbers. Extensive work in number theory has managed to establish only a few properties of these. It is for example known that (d) never reaches zero, while curve (c) reaches zero only for numbers of the form 4^r (8s + 7). Sequence (b) is zero at so-called perfect numbers. Even perfect numbers always have a known form, but whether any odd perfect numbers exist is a question that has remained unresolved for more than two thousand years. The claim that sequence (e) never reaches zero is known as Goldbach's Conjecture. It was made in 1742 but no proof or counterexample has ever been found.