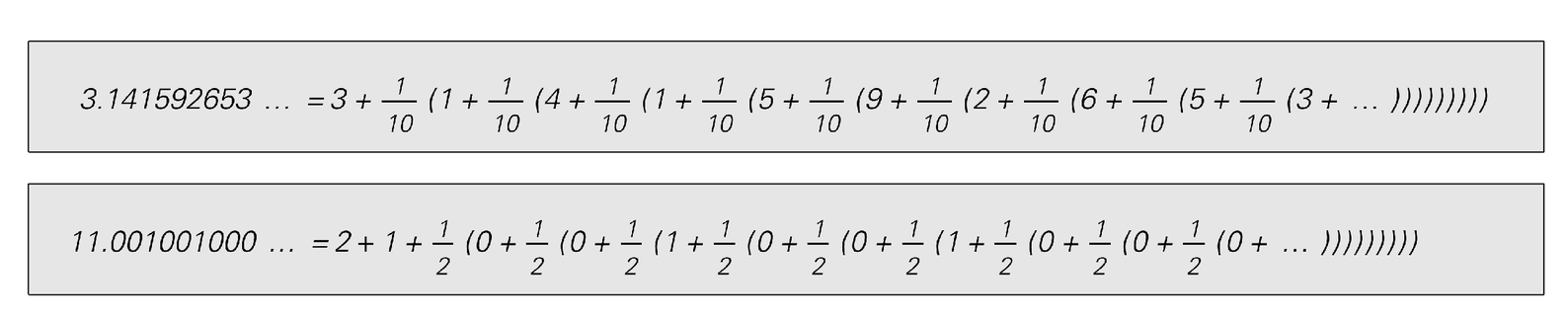
By replacing the addition and multiplication that appear in the first picture by other operations one can then get other representations for numbers. A common example are so-called continued fraction representations, in which the operations of addition and division are used, as shown in the second picture.

The table on the next page gives the continued fraction representations for various numbers. In the case of rational numbers, the results are always of limited length. But for other numbers, they go on forever. Square roots turn out to have purely repetitive continued fraction representations. And the representations of  ≃ 2.718 and all its roots also show definite regularity. But for π, as well as for cube roots, fourth roots, and so on, the continued fraction representations one gets seem essentially random.

What about other representations of numbers? At some level, one can always use symbolic expressions like √2 + ^√3 to represent numbers. And almost by definition, numbers that can be obtained by simple mathematical operations will correspond to simple such expressions. But the problem is that there is no telling how difficult it may be to compute the actual value of a number from the symbolic expression that is used to represent it.

And in thinking about representations of numbers, it seems appropriate to restrict oneself to cases where the effort required to find the value of a number from its representation is essentially the same for

Procedures for building up π from its base 10 and base 2 digit sequence representations.

The continued fraction representation of π. In this representation the value of π is built up by successive additions and divisions, rather than successive additions and multiplications.