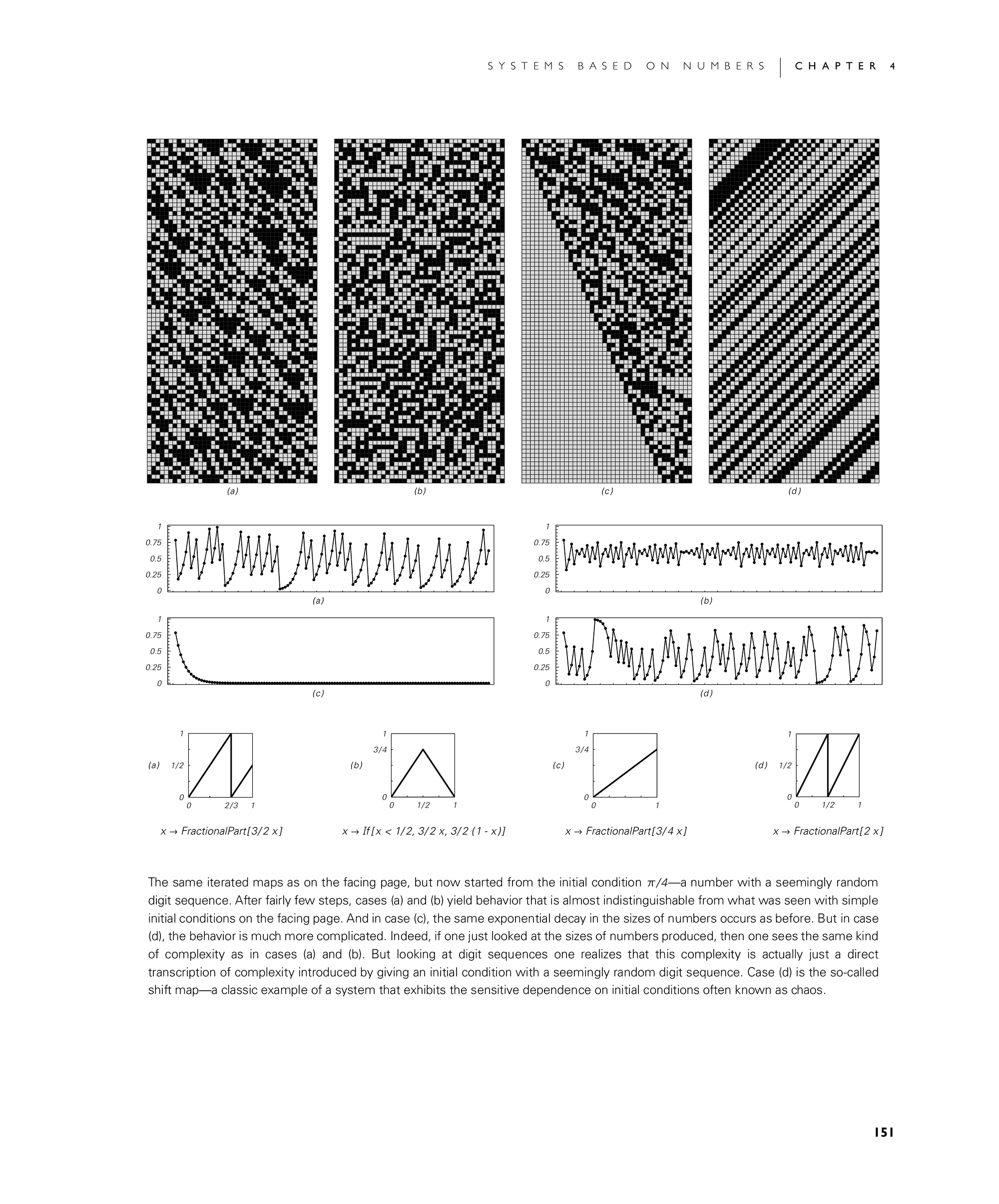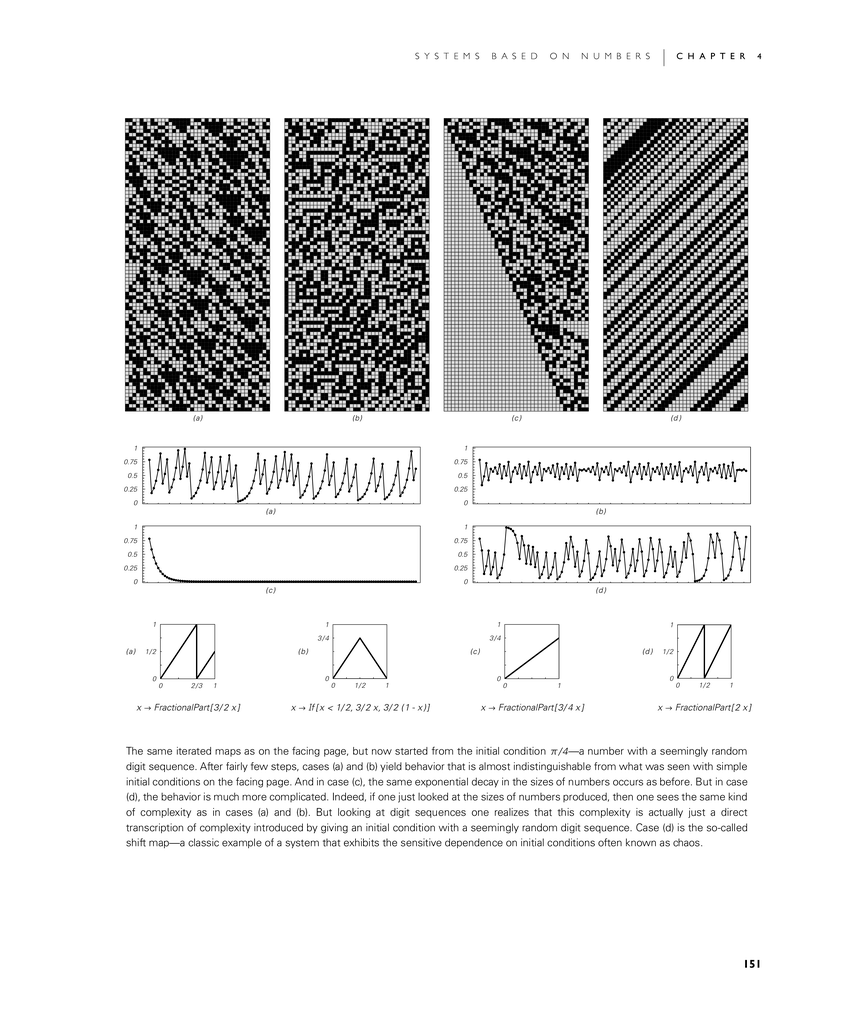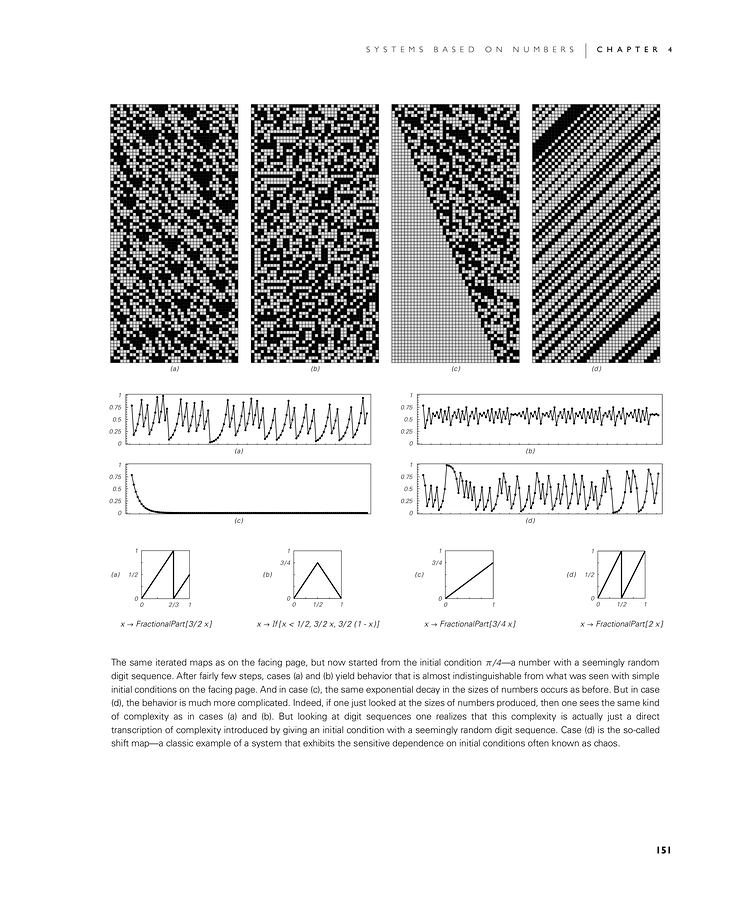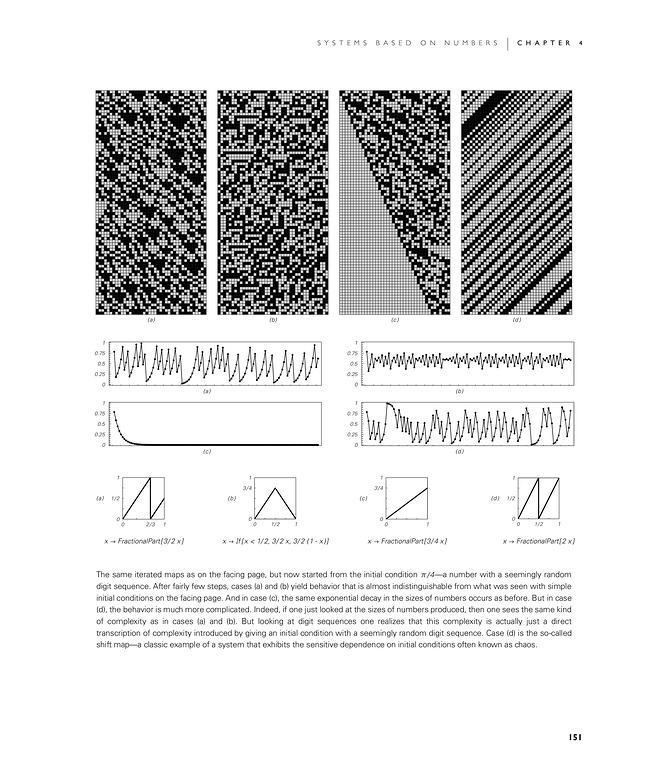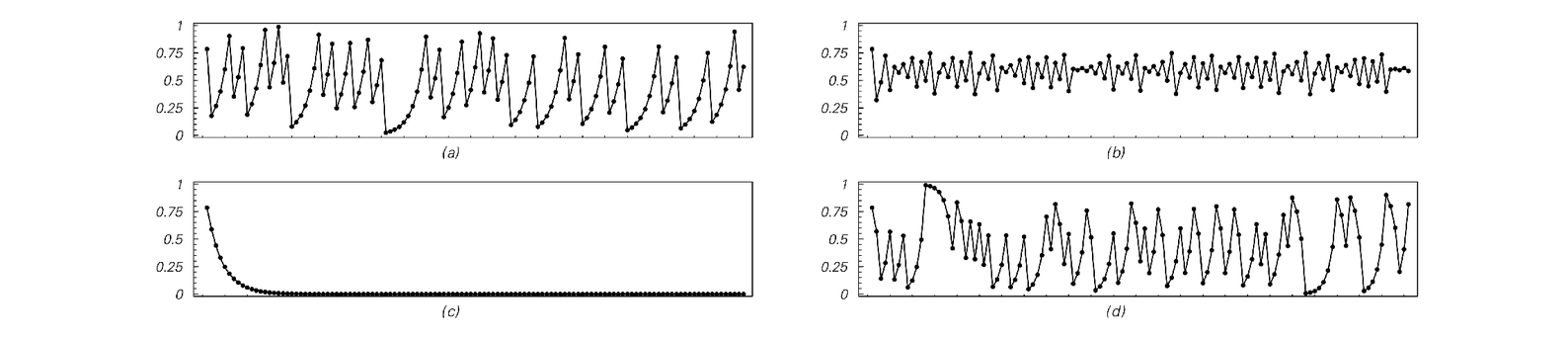
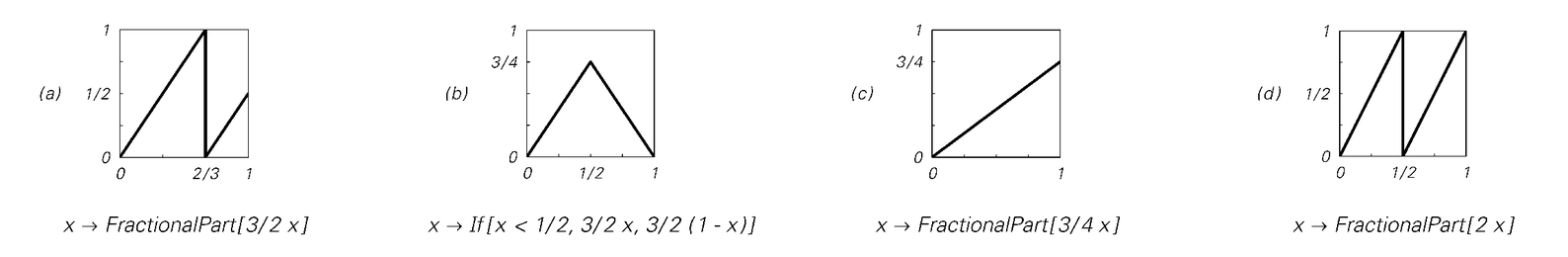
The same iterated maps as on the facing page, but now started from the initial condition π/4—a number with a seemingly random digit sequence. After fairly few steps, cases (a) and (b) yield behavior that is almost indistinguishable from what was seen with simple initial conditions on the facing page. And in case (c), the same exponential decay in the sizes of numbers occurs as before. But in case (d), the behavior is much more complicated. Indeed, if one just looked at the sizes of numbers produced, then one sees the same kind of complexity as in cases (a) and (b). But looking at digit sequences one realizes that this complexity is actually just a direct transcription of complexity introduced by giving an initial condition with a seemingly random digit sequence. Case (d) is the so-called shift map—a classic example of a system that exhibits the sensitive dependence on initial conditions often known as chaos.