Traditional science tends to suggest that allowing more than one dimension will have very important consequences. Indeed, it turns out that many of the phenomena that have been most studied in traditional science simply do not occur in just one dimension.

Phenomena that involve geometrical shapes, for example, usually require at least two dimensions, while phenomena that rely on the existence of knotted structures require three dimensions. But what about the phenomenon of complexity? How much does it depend on dimension?

It could be that in going beyond one dimension the character of the behavior that we would see would immediately change. And indeed in the course of this chapter, we will come across many examples of specific effects that depend on having more than one dimension.

But what we will discover in the end is that at an overall level the behavior we see is not fundamentally much different in two or more dimensions than in one dimension. Indeed, despite what we might expect from traditional science, adding more dimensions does not ultimately seem to have much effect on the occurrence of behavior of any significant complexity.

Cellular Automata

The cellular automata that we have discussed so far in this book are all purely one-dimensional, so that at each step, they involve only a single line of cells. But one can also consider two-dimensional cellular automata that involve a whole grid of cells, with the color of each cell being updated according to a rule that depends on its neighbors in all four directions on the grid, as in the picture below.

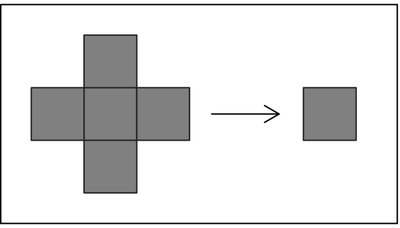
The form of the rule for a typical two-dimensional cellular automaton. In the cases discussed in this section, each cell is either black or white. Usually I consider so-called totalistic rules in which the new color of the center cell depends only on the average of the previous colors of its four neighbors, as well as on its own previous color.