Yet if one sets up elements on a grid it is straightforward to allow the replacements for a given element to depend on its neighbors, as in the picture at the top of the next page. And if one does this, one immediately gets all sorts of fairly complicated patterns that are often not just purely nested—as illustrated in the pictures on the next page.
In Chapter 3 we discussed both ordinary one-dimensional substitution systems, in which every element is replaced at each step, and sequential substitution systems, in which just a single block of elements are replaced at each step. And what we did to find which block of elements should be replaced at a given step was to scan the whole sequence of elements from left to right.
 |  |
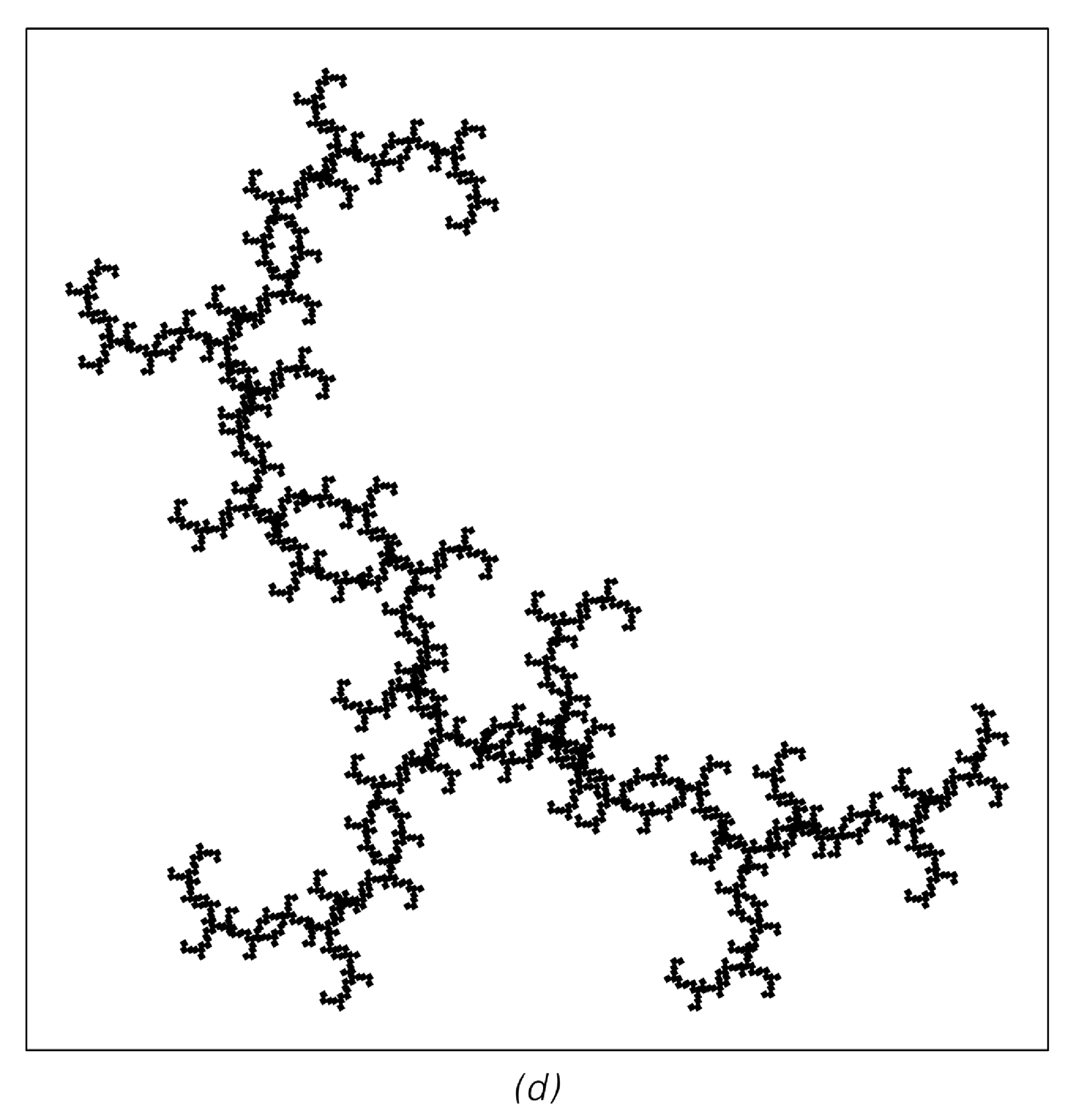 | 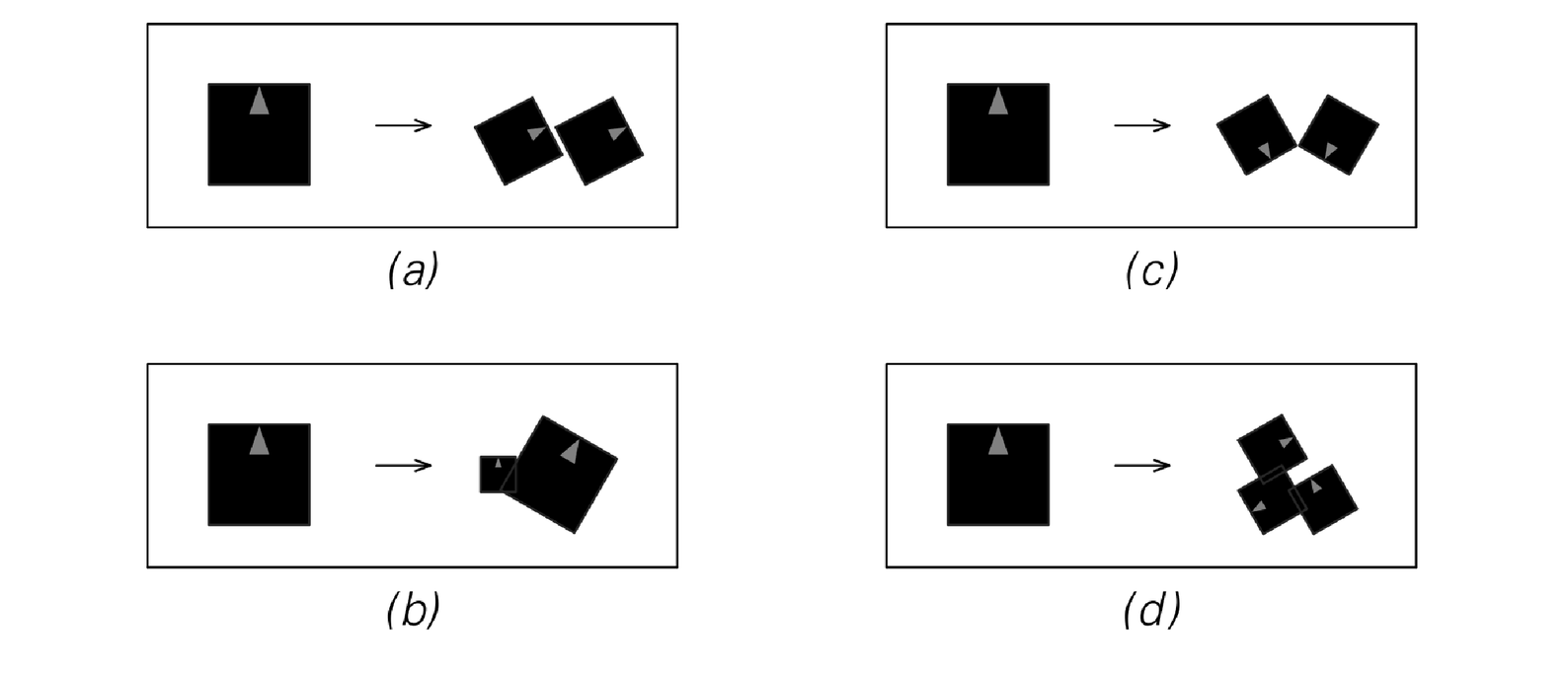 |
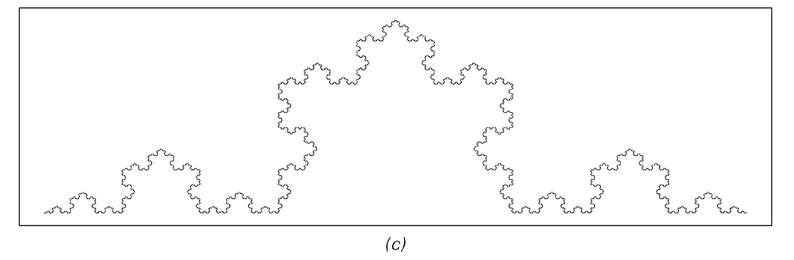
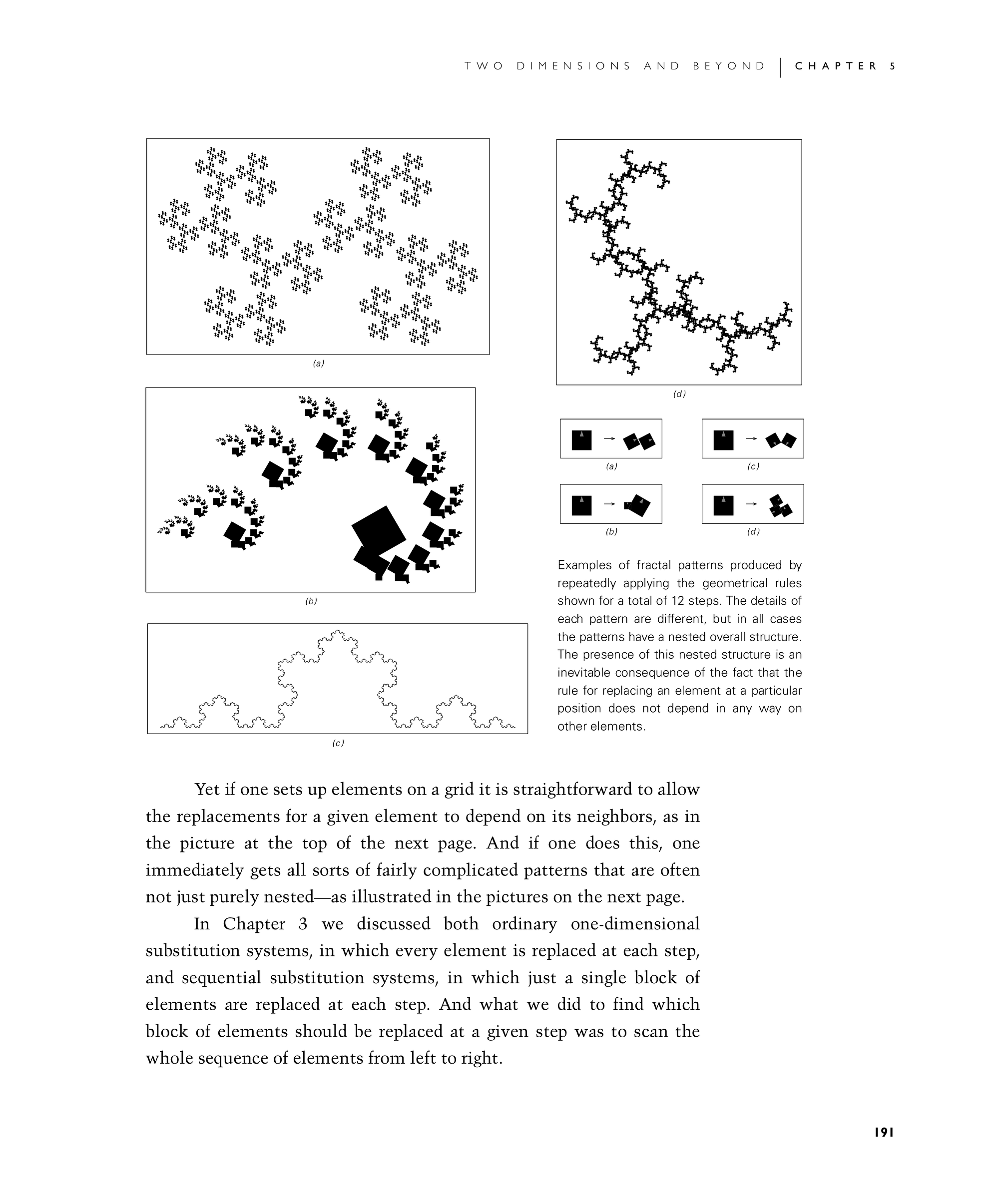
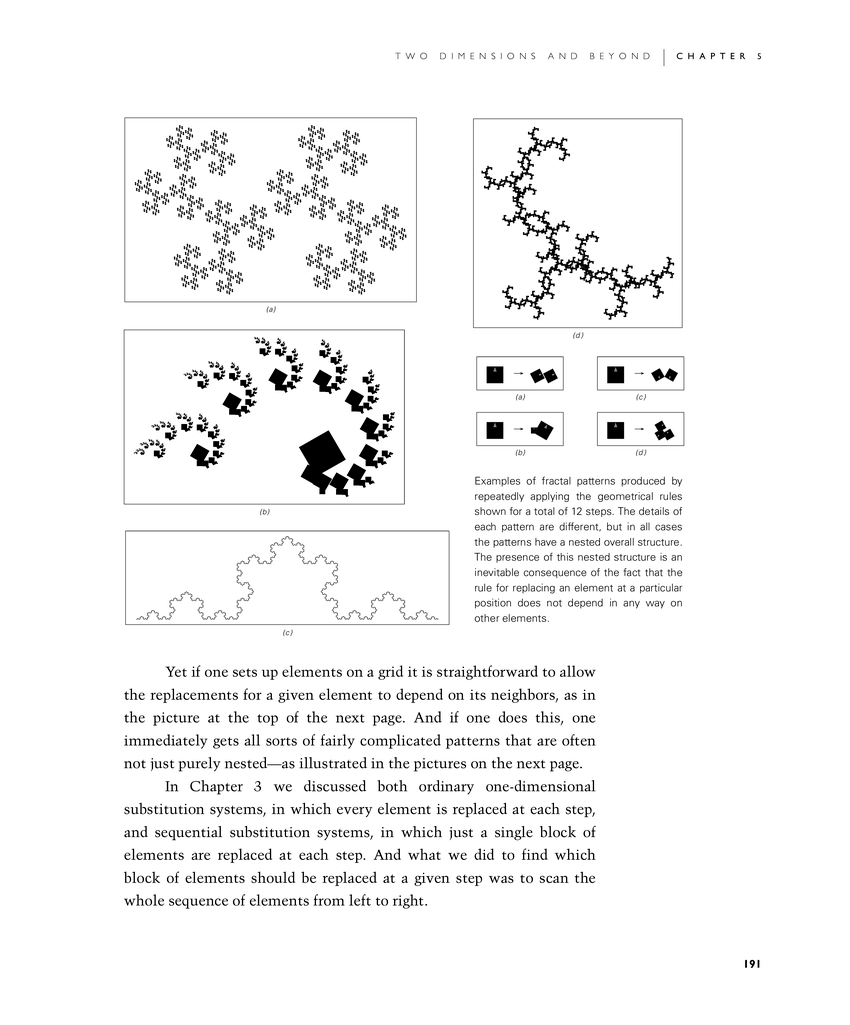
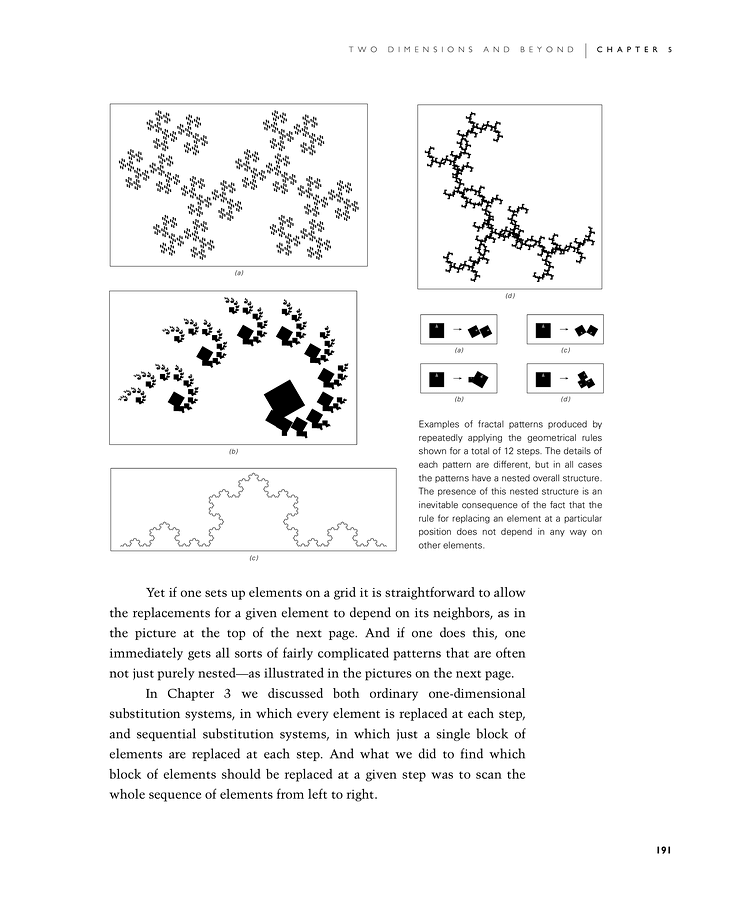
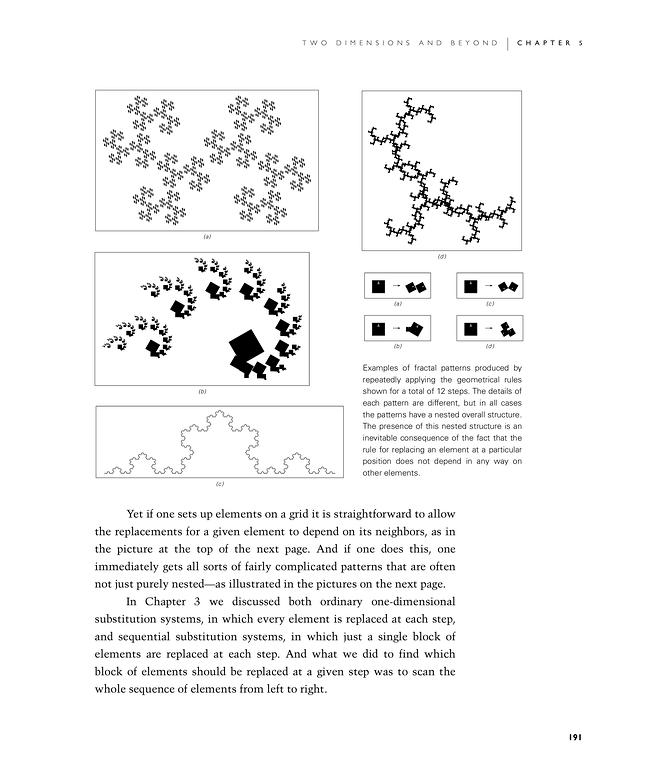
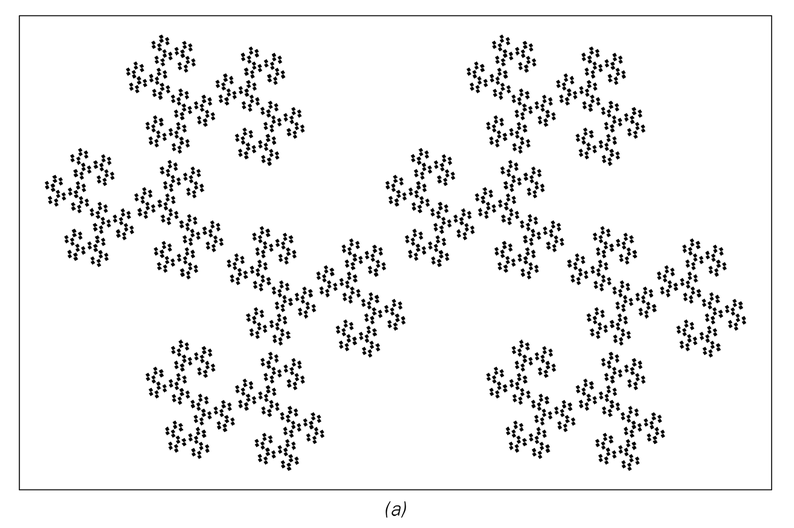
Examples of fractal patterns produced by repeatedly applying the geometrical rules shown for a total of 12 steps. The details of each pattern are different, but in all cases the patterns have a nested overall structure. The presence of this nested structure is an inevitable consequence of the fact that the rule for replacing an element at a particular position does not depend in any way on other elements.