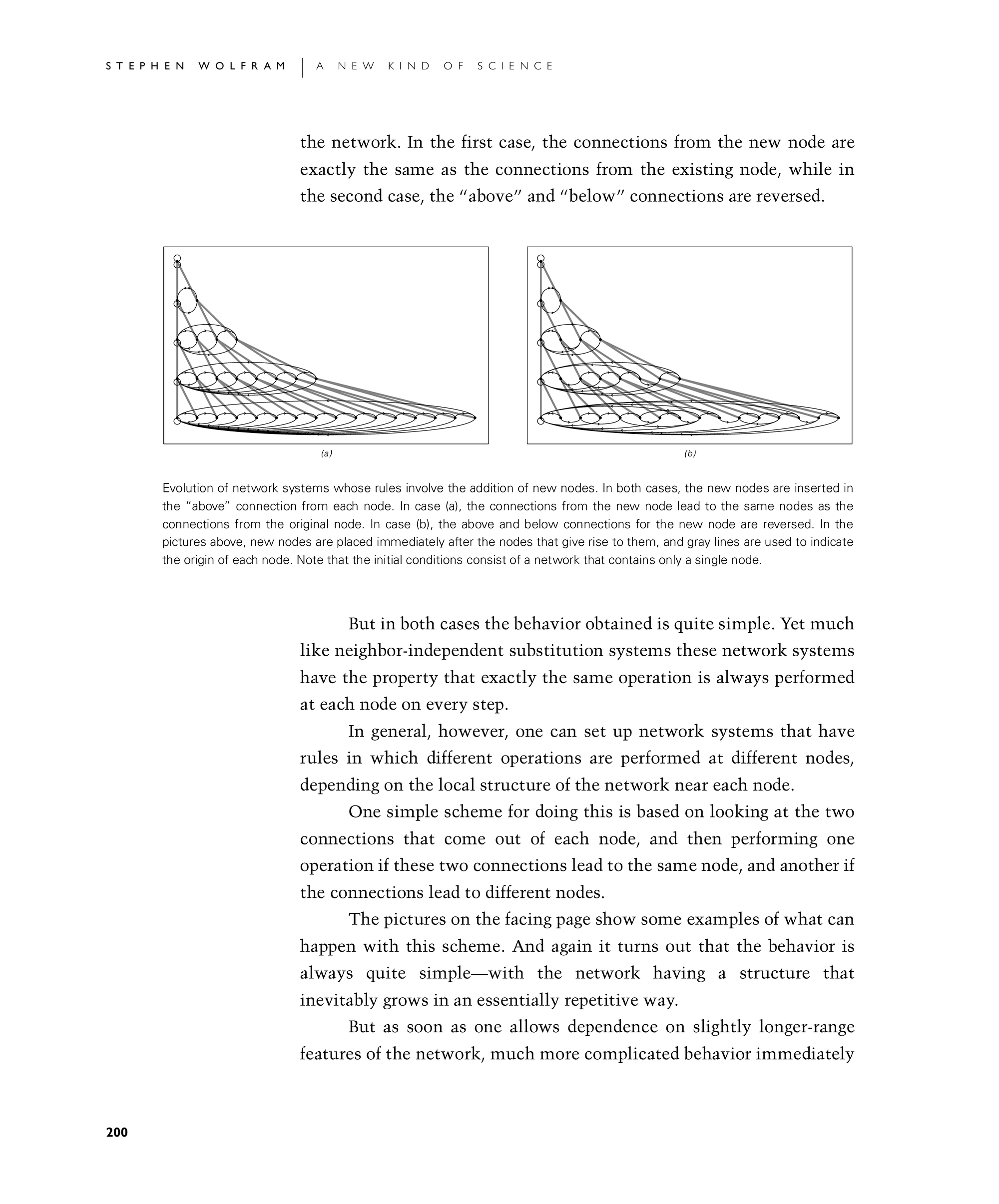
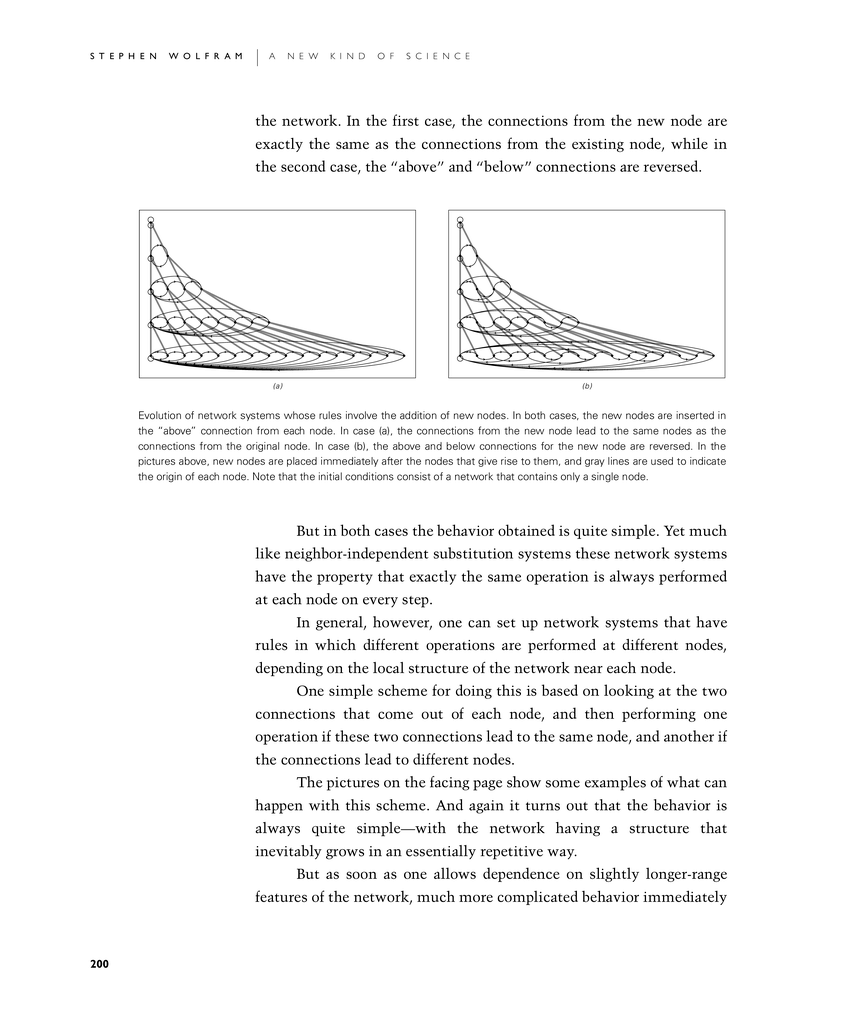
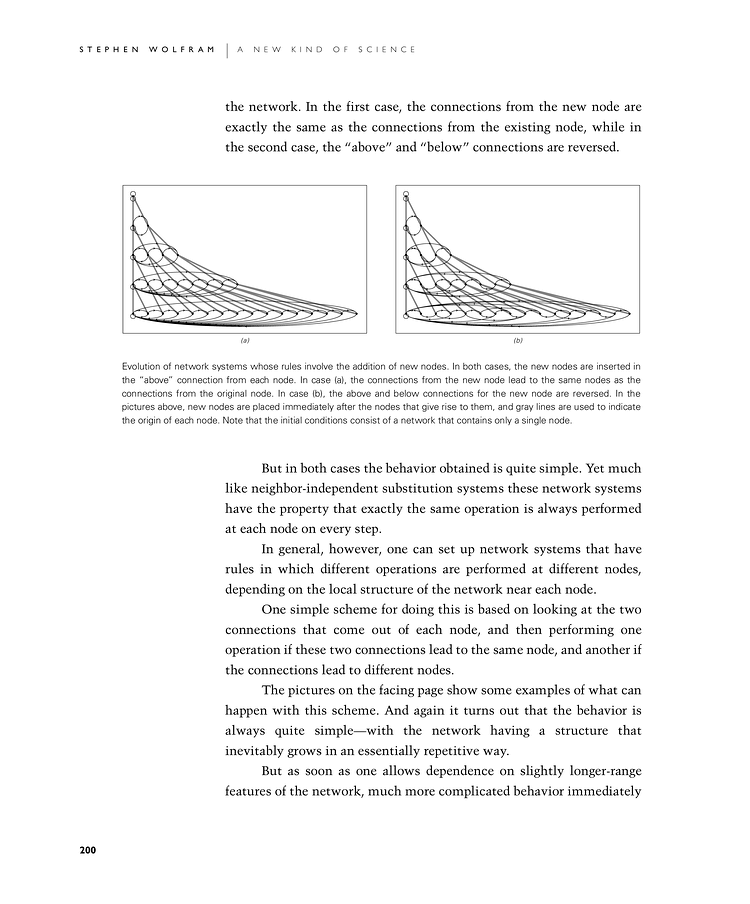
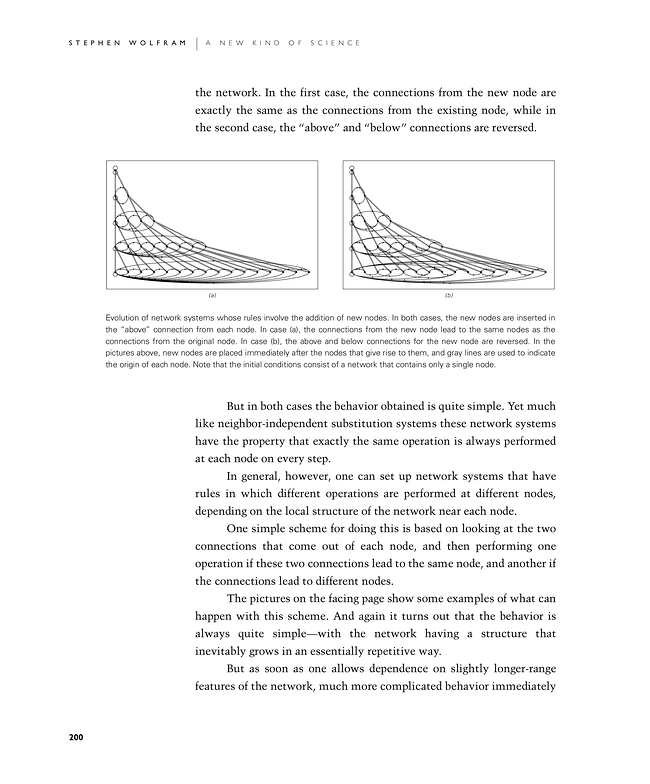
the network. In the first case, the connections from the new node are exactly the same as the connections from the existing node, while in the second case, the "above" and "below" connections are reversed.
But in both cases the behavior obtained is quite simple. Yet much like neighbor-independent substitution systems these network systems have the property that exactly the same operation is always performed at each node on every step.
In general, however, one can set up network systems that have rules in which different operations are performed at different nodes, depending on the local structure of the network near each node.
One simple scheme for doing this is based on looking at the two connections that come out of each node, and then performing one operation if these two connections lead to the same node, and another if the connections lead to different nodes.
The pictures on the facing page show some examples of what can happen with this scheme. And again it turns out that the behavior is always quite simple—with the network having a structure that inevitably grows in an essentially repetitive way.
But as soon as one allows dependence on slightly longer-range features of the network, much more complicated behavior immediately
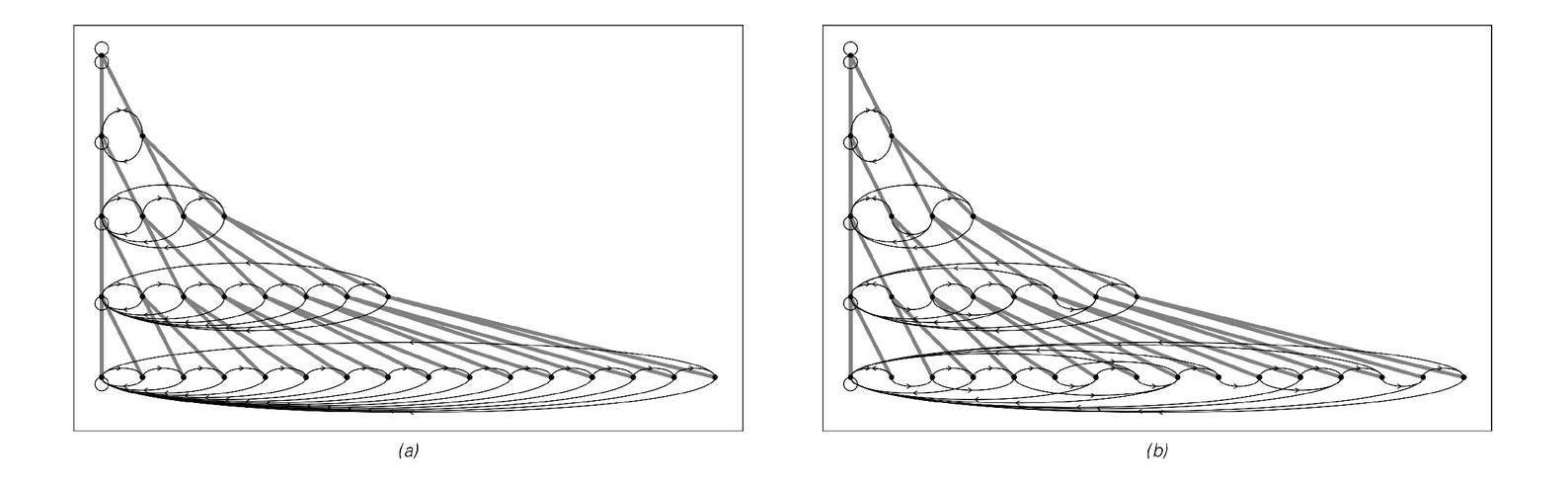
Evolution of network systems whose rules involve the addition of new nodes. In both cases, the new nodes are inserted in the "above" connection from each node. In case (a), the connections from the new node lead to the same nodes as the connections from the original node. In case (b), the above and below connections for the new node are reversed. In the pictures above, new nodes are placed immediately after the nodes that give rise to them, and gray lines are used to indicate the origin of each node. Note that the initial conditions consist of a network that contains only a single node.