If one looks at many multiway systems, most either grow exponentially quickly, or not at all; slow growth of the kind seen on the facing page is rather rare. And indeed even when such growth leads to a certain amount of apparent randomness it typically in the end seems to exhibit some form of repetition. If one allows more rapid growth, however, then there presumably start to be all sorts of multiway systems that never show any such regularity. But in practice it tends to be rather difficult to study these kinds of multiway systems—since the number of states they generate quickly becomes too large to handle.
One can get some idea about how such systems behave, however, just by looking at the states that occur at early steps. The picture below shows an example—with ultimately fairly simple nested behavior.
The pictures on the next page show some more examples. Sometimes the set of states that get generated at a particular step show essential repetition—though often with a long period. Sometimes this set in effect includes a large fraction of the possible digit sequences of a given length—and so essentially shows nesting. But in other cases there is at least a hint of considerably more complexity—even though the total number of states may still end up growing quite smoothly.
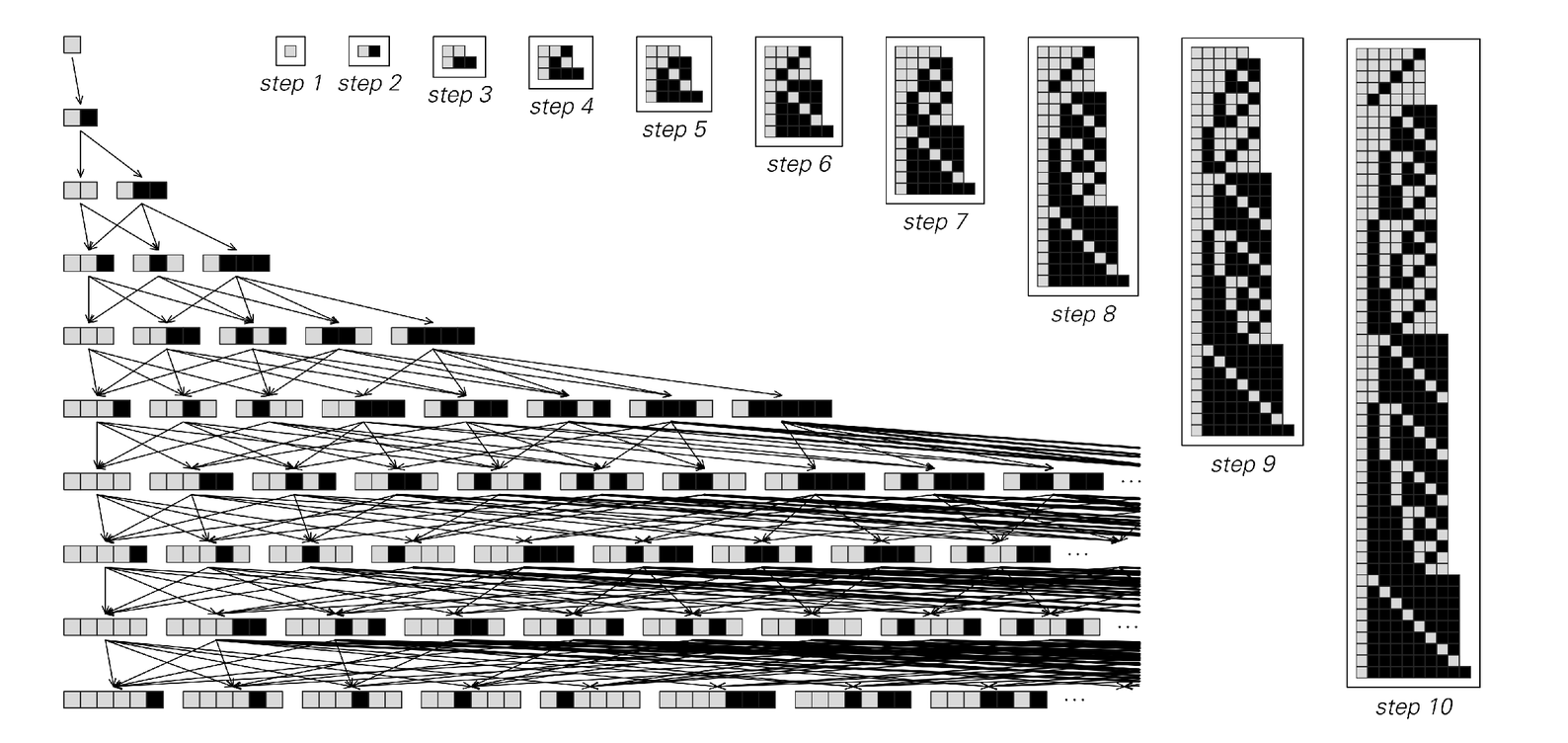
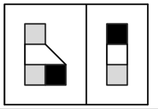
The collections of states generated on successive steps by a simple multiway system with rapid growth shown on page 205. The particular rule used here eventually generates all states beginning with a white cell. At step t there are Fibonacci[t+1] states; a given state with m white cells and n black cells appears at step 2m+n-1.



