What about still more complex behavior?
There are altogether 137,438,953,472 constraints of the type shown on page 216. And of the millions of these that I have tested, none have forced anything more complicated than the kind of nested behavior seen on the previous page. But if one extends again the type of constraints one considers, it turns out to become possible to construct examples that force more complex behavior.
The idea is to set up templates that involve complete 3×3 blocks of cells, including diagonal neighbors. The picture below then shows an example of such a system, in which by allowing only a specific set of 33 templates, a nested pattern is forced to occur.
What about more complex patterns? Searches have not succeeded in finding anything. But explicit construction, based on correspondence with one-dimensional cellular automata, leads to the example shown at the top of the facing page: a system with 56 allowed templates in which the only pattern satisfying the constraint is a complex and largely random one, derived from the rule 30 cellular automaton.
 | 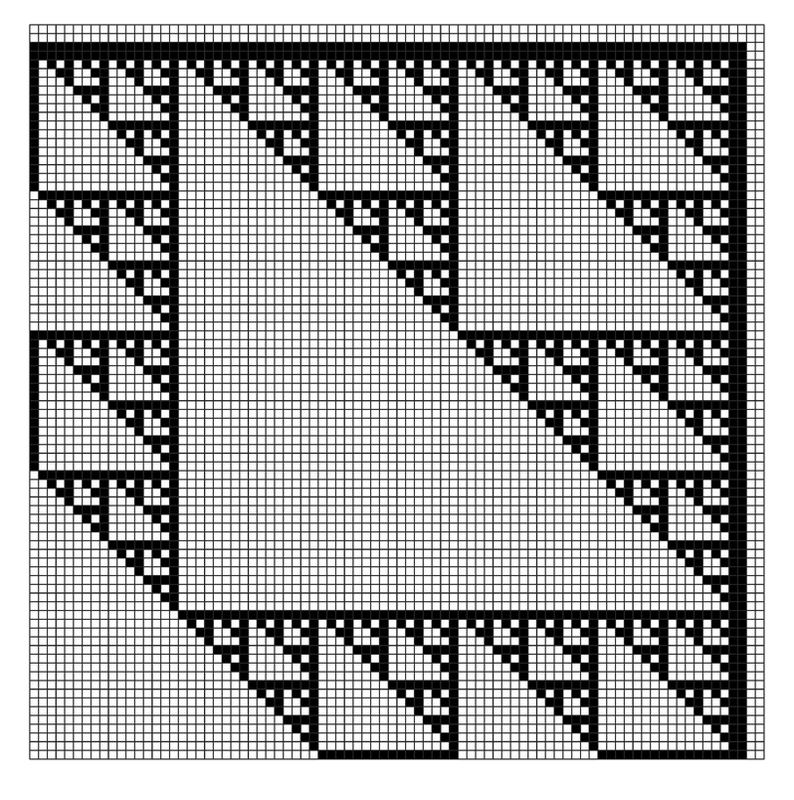 |
An example of a system based on a constraint involving 3×3 templates of cells. In this particular system, only the 33 templates shown above (out of the 512 possible ones) are allowed to occur. This constraint, together with the requirement that the first template must appear at least somewhere, then turns out to force a nested pattern to occur. The system shown was specifically constructed in correspondence with the rule 60 elementary one-dimensional cellular automaton.



