Looking at the pictures we then see that the behavior which results is always purely repetitive—though the period of repetition is different in different cases. And the basic reason for the repetitive behavior is that whenever the dot ends up in a particular position, it must always repeat whatever it did when it was last in that position.
But since there are only six possible positions in all, it is inevitable that after at most six steps the dot will always get to a position where it has been before. And this means that the behavior must repeat with a period of at most six steps.
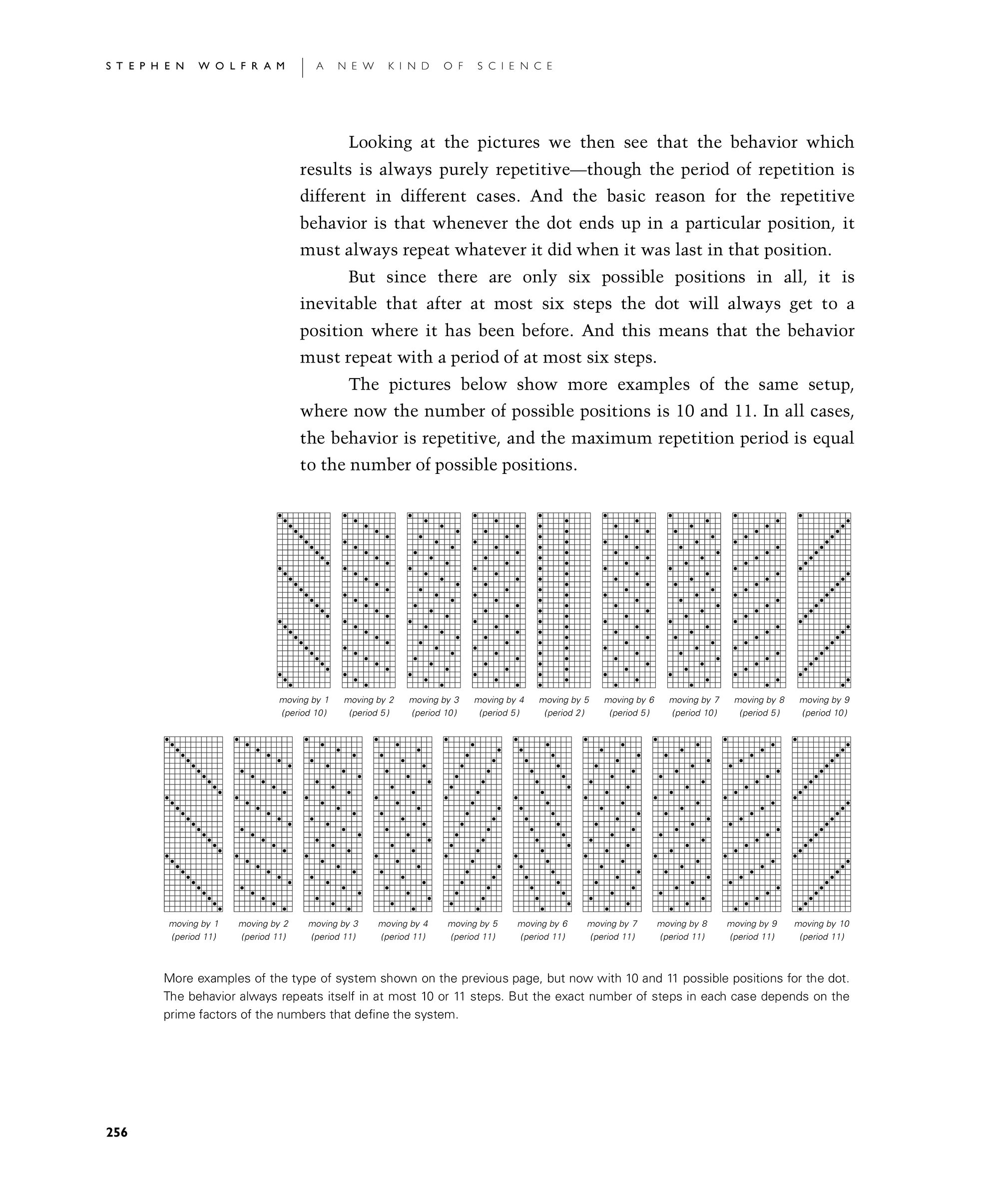
The pictures below show more examples of the same setup, where now the number of possible positions is 10 and 11. In all cases, the behavior is repetitive, and the maximum repetition period is equal to the number of possible positions.

More examples of the type of system shown on the previous page, but now with 10 and 11 possible positions for the dot. The behavior always repeats itself in at most 10 or 11 steps. But the exact number of steps in each case depends on the prime factors of the numbers that define the system.