There are however a few cellular automata in which class 3 behavior is obtained with random initial conditions, but in which no significant randomness is ever produced with simple initial conditions.

The pictures below show one example. And in this case it turns out that all patterns are in effect just simple superpositions of the basic nested pattern that is obtained by starting with a single black cell.

As a result, when the initial conditions involve only a limited region of black cells, the overall pattern produced always ultimately has a simple nested form. Indeed, at each of the steps where a new white triangle starts in the center, the whole pattern consists just of two copies of the region of black cells from the initial conditions.

The only way to get a random pattern therefore is to have an infinite number of randomly placed black cells in the initial conditions.

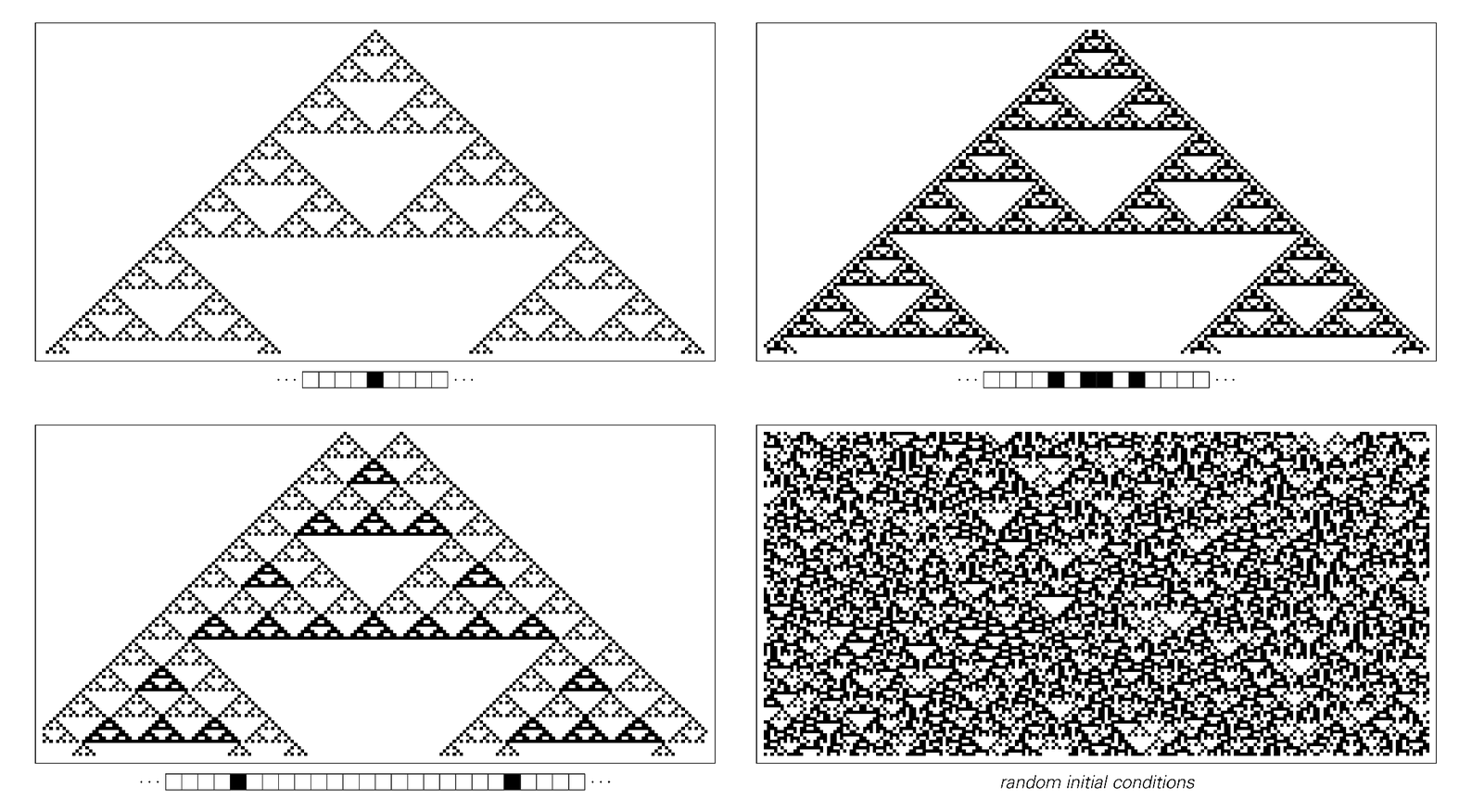
Patterns generated by rule 90 with various initial conditions. This particular cellular automaton rule has the special property of additivity which implies that with any initial conditions the patterns that it produces can be obtained as simple superpositions of the first pattern shown above. Any initial condition that contains black cells only in a limited region will thus lead to a pattern that ultimately has a simple nested form. Unlike rule 30 or rule 22 therefore, rule 90 cannot intrinsically generate randomness starting from simple initial conditions. The randomness in the last picture shown here is thus purely a consequence of the randomness in its initial conditions. Note that the pictures above show only half as many steps of evolution as the corresponding pictures of rule 22 on the previous page.